
【题目】在△ABC中,AD平分∠BAC,E是BC上一点,BE=CD,EF∥AD交AB于F点,交CA的延长线于P,CH∥AB交AD的延长线于点H,
①求证:△APF是等腰三角形;
②猜想AB与PC的大小有什么关系?证明你的猜想.
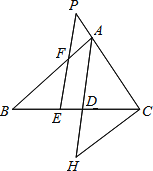
【答案】①证明见解析;②AB=PC.
【解析】
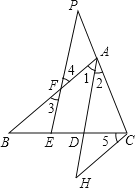
①根据题意作出图形,根据两直线平行,内错角相等可得∠1=∠4,同位角相等可得∠2=∠P,再根据角平分线的定义可得∠1=∠2,然后求出∠4=∠P,根据等角对等边的性质即可得证;
②根据两直线平行,内错角相等可得∠5=∠B,再求出∠H=∠1=∠3,然后利用“AAS”证明△BEF和△CDH全等,根据全等三角形对应边相等可得BF=CH,再求出AC=CH,再根据AB=AF+BF,PC=AP+AC,整理即可得解.
①证明:∵EF∥AD,
∴∠1=∠4,∠2=∠P,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠4=∠P,
∴AF=AP,
即△APF是等腰三角形;
②AB=PC.理由如下:
证明:∵CH∥AB,
∴∠5=∠B,∠H=∠1,
∵EF∥AD,
∴∠1=∠3,
∴∠H=∠3,
在△BEF和△CDH中,
∵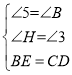 ,
,
∴△BEF≌△CDH(AAS),
∴BF=CH,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠2=∠H,
∴AC=CH,
∴AC=BF,
∵AB=AF+BF,PC=AP+AC,
∴AB=PC.


科目:初中数学 来源: 题型:
【题目】石狮泰禾某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售______ 件,每件盈利______ 元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
(1)求出y关于x的函数解析式,并直接写出自变量的取值范围;
(2)此时金色纸边的宽应为多少cm时,这幅挂图的面积最大?求出最大面积的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AB⊥BC,AB=BC,AB>CD,AE⊥BD于E交BC于F.

(1)若AB=2CD;
①求证:BC=2BF;
②连CE,若DE=6,CE=![]() ,求EF的长;
,求EF的长;
(2)若AB=6,则CE的最小值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com