
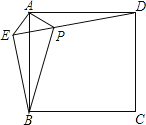
【题目】如图,点E是正方形ABCD外一点,连接AE、BE和DE,过点A作AE的垂线交DE于点P.若AE=AP=1,PB=3.下列结论:①△APD≌△AEB;②EB⊥ED;③点B到直线AE的距离为![]() ;④S正方形ABCD=8+
;④S正方形ABCD=8+![]() .则正确结论的个数是( )
.则正确结论的个数是( )
A.1B.2C.3D.4
【答案】C
【解析】
①易知AE=AP,AB=AD,所以只需证明∠EAB=∠PAD即可用SAS说明△APD≌△AEB;
②易知∠AEB=∠APD=135°,则∠BEP=∠AEB﹣∠AEP=135°﹣45°=90°,所以EB⊥ED;
③在Rt△BEP中利用勾股定理求出BE值为![]() ,根据垂线段最短可知B到直线AE的距离小于
,根据垂线段最短可知B到直线AE的距离小于![]() ;则③错误;
;则③错误;
④要求正方形的面积,则需知道正方形一条边的平方值即可,所以在△AEB中,∠AEB=135°,AE=1,BE=![]() ,过点A作AH⊥BE交BE延长线于H点,在Rt△AHB中利用勾股定理AB2=BH2+AH2即可.
,过点A作AH⊥BE交BE延长线于H点,在Rt△AHB中利用勾股定理AB2=BH2+AH2即可.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°.
∴∠DAP+∠BAP=90°.
又∠EAP+∠BAP=90°,
∴∠EAP=∠DAP.
又AE=AP,
∴△APD≌△AEB(SAS).
所以①正确;
∵AE=AP,∠EAP=90°,
∴∠APE=∠AEP=45°,
∴∠APD=180°﹣45°=135°.
∵△APD≌△AEB,
∴∠AEB=∠APD=135°,
∴∠BEP=135°﹣45°=90°,
即EB⊥ED,②正确;
在等腰Rt△AEP中,利用勾股定理可得EP=![]() ,
,
在Rt△BEP中,利用勾股定理可得BE=![]() .
.
∵B点到直线AE的距离小于BE,所以点B到直线AE的距离为![]() 是错误的,
是错误的,
所以③错误;
在△AEB中,∠AEB=135°,AE=1,BE=![]() ,
,
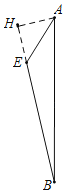
如图所示,过点A作AH⊥BE交BE延长线于H点.
在等腰Rt△AHE中,可得AH=HE=![]() AE=
AE=![]() .
.
所以BH=![]() .
.
在Rt△AHB中利用勾股定理可得AB2=BH2+AH2,
即AB2=(![]() )2+(
)2+(![]() )2=8+
)2=8+![]() ,
,
所以S正方形ABCD=8+![]() .
.
所以④正确.
所以只有①和②、④的结论正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】教室里有4排日光灯,每排灯各由一个开关控制,但灯的排数序号与开关序号不一定对应,其中控制第二排灯的开关已坏(闭合开关时灯也不亮).
(1)将4个开关都闭合时,教室里所有灯都亮起的概率是 ;
(2)在4个开关都闭合的情况下,不知情的雷老师准备做光学实验,由于灯光太强,他需要关掉部分灯,于是随机将4个开关中的2个断开,请用列表或画树状图的方法,求恰好关掉第一排与第三排灯的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建立模型:
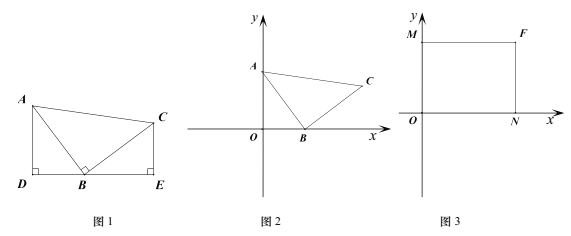
如图1,等腰Rt△ABC中,∠ABC=90°,CB=BA,直线ED经过点B,过A作AD⊥ED于D,过C作CE⊥ED于E.则易证△ADB≌△BEC.这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角∠ABC转化为横平竖直的线段和直角,所以在平面直角坐标系中被大量使用.
模型应用:
(1)如图2,点A(0,4),点B(3,0),△ABC是等腰直角三角形.
①若∠ABC=90°,且点C在第一象限,求点C的坐标;
②若AB为直角边,求点C的坐标;
(2)如图3,长方形MFNO,O为坐标原点,F的坐标为(8,6),M、N分别在坐标轴上,P是线段NF上动点,设PN=n,已知点G在第一象限,且是直线y=2x一6上的一点,若△MPG是以G为直角顶点的等腰直角三角形,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P的坐标为(-3,4),作出点P关于x轴对称的点P1,称为第1次变换;再作出点P1关于y轴对称的点P2,称为第2次变换;再作点P2关于x轴对称的点P3,称为第3次变换,…,依次类推,则第2019次变换得到的点P2019的坐标为 ____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
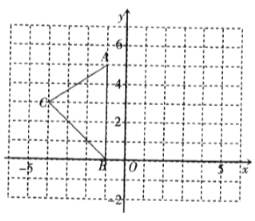
【题目】如图,在平面直角坐标系中,![]() 、
、![]() 、
、![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的
轴对称的![]() (其中
(其中![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点)并直接写出
的对应点)并直接写出![]() 点的坐标为 .
点的坐标为 .
(2)若直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,则点
轴平行,则点![]() 关于直线
关于直线![]() 的对称点的坐标为 .
的对称点的坐标为 .
(3)在![]() 轴上存在一点
轴上存在一点![]() ,使
,使![]() 最大,则点
最大,则点![]() 的坐标为 .
的坐标为 .
(4)第一象限有一点![]() ,在
,在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最短,画出最短路径,保留作图迹.
最短,画出最短路径,保留作图迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的取值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
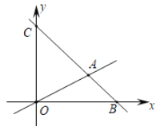
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)直线![]() 的关系式为 ;直线
的关系式为 ;直线![]() 的关系式为 (直接写出答案,不必写过程).
的关系式为 (直接写出答案,不必写过程).
(2)求![]() 的面积.
的面积.
(3)若有一动点![]() 沿路线
沿路线![]() 运动,当
运动,当![]() 时,求点
时,求点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
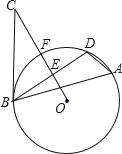
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
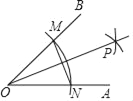
【题目】已知∠AOB=45°,求作∠AOP=22.5°,作法:
(1)以O为圆心,任意长为半径画弧分别交OA,OB于点N,M;
(2)分别以N,M为圆心,以OM长为半径在角的内部画弧交于点P;
(3)作射线OP,则OP为∠AOB的平分线,可得∠AOP=22.5°
根据以上作法,某同学有以下3种证明思路:
①可证明△OPN≌△OPM,得∠POA=∠POB,可得;
②可证明四边形OMPN为菱形,OP,MN互相垂直平分,得∠POA=∠POB,可得;
③可证明△PMN为等边三角形,OP,MN互相垂直平分,从而得∠POA=∠POB,可得.
你认为该同学以上3种证明思路中,正确的有( )
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com