[题目]在等腰△ABC中.AB=AC.AC腰上的中线BD将三角形周长分为15和21两部分.则这个三角形的底边长为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】在等腰△ABC中，AB=AC，AC腰上的中线BD将三角形周长分为15和21两部分，则这个三角形的底边长为______．

【答案】16或8

【解析】

本题由题意可知有两种情况，AB+AD=15或AB+AD=21．从而根据等腰三角形的性质及三角形三边关系可求出底边为8或16．

解：∵BD是等腰△ABC的中线，可设AD=CD=x，则AB=AC=2x，

又知BD将三角形周长分为15和21两部分，

∴可知分为两种情况

①AB+AD=15，即3x=15，解得x=5，此时BC=21﹣x=21﹣5=16；

②AB+AD=21，即3x=21，解得x=7；此时等腰△ABC的三边分别为14，14，8．

经验证，这两种情况都是成立的．

∴这个三角形的底边长为8或16．

故答案为：16或8．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛，计分采用10分制，选手得分均为整数，成绩达到6分或6分以上为合格，达到9分或10分为优秀．这次竞赛后，七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下，其中七年级代表队得6分、10分的选手人数分别为a，b．

队别	平均分	中位数	方差	合格率	优秀率
七年级	6.7	m	3.41	90%	n
八年级	7.1	7.5	1.69	80%	10%

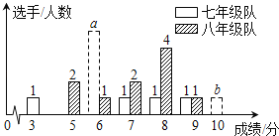
（1）请依据图表中的数据，求a，b的值；

（2）直接写出表中的m，n的值；

（3）有人说七年级的合格率、优秀率均高于八年级，所以七年级队成绩比八年级队好，但也有人说八年级队成绩比七年级队好．请你给出两条支持八年级队成绩好的理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，推理填空：

(1)∵∠1＝_______(已知)，

∴AC∥ED(同位角相等，两直线平行)．

(2)∵∠2＝______(已知)，

∴AB∥FD(内错角相等，两直线平行)．

(3)∵∠2＋_______＝180°(已知)，

∴AC∥ED(同旁内角互补，两直线平行)．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如果一个三角形能被一条线段分割成两个等腰三角形，那么称这条线段为这个三角形的特异线，称这个三角形为特异三角形．

（1）如图1，△ABC中，∠B=2∠C，线段AC的垂直平分线交AC于点D，交BC于点E．求证：AE是△ABC的一条特异线．
（2）如图2，已知△ABC是特异三角形，且∠A=30°，∠B为钝角，求出所有可能的∠B的度数．
（3）如图3，△ABC是一个腰长为2的等腰锐角三角形，且它是特异三角形，若它的顶角度数为整数，请求出其特异线的长度；若它的顶角度数不是整数，请直接写出顶角度数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】有两种包装盒，大盒比小盒可多装20克某一物品．已知120克这一物品单独装满小盒比单独装满大盒多1盒．
（1）问小盒每个可装这一物品多少克？
（2）现有装满这一物品两种盒子共50个．设小盒有n个，所有盒子所装物品的总量为w克． ①求w关于n的函数解析式，并写出定义域；
②如果小盒所装物品总量与大盒所装物品总量相同，求所有盒子所装物品的总量．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，平面直角坐标系中，平行四边形OABC的顶点C（3，4），边OA落在x正半轴上，P为线段AC上一点，过点P分别作DE∥OC，FG∥OA交平行四边形各边如图．若反比例函数的图象经过点D，四边形BCFG的面积为8，则k的值为（）

A.16
B.20
C.24
D.28