
【题目】某网店正在热销一款电子产品,其成本为10元/件,销售中发现,该商品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的关系:
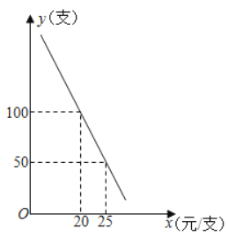
(1)请求出y与x之间的函数关系式;
(2)该款电子产品的销售单价为多少元时,每天销售利润最大?最大利润是多少元;
(3)由于武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出300元捐赠给武汉,为了保证捐款后每天剩余利润不低于450元,如何确定该款电子产品的销售单价?
【答案】(1)y=10x+300;(2)20元时,最大利润为1000元;(3)单价每件不低于15元,且不高于25元.
【解析】
(1)利用待定系数法求解可得;
(2)设该款电子产品每天的销售利润为w元,根据“总利润=每件的利润×销售量”可得函数解析式,配方成顶点式后利用二次函数的性质求解可得;
(3)设捐款后每天剩余利润为z元,根据题意得出z=10x2+400x3000300=10x2+400x3300,求出z=450时的x的值,求解可得.
解:(1)设y与x的函数关系式为y=kx+b,
将(20,100),(25,50)代入y=kx+b,
得![]() ,
,
解得![]() ,
,
∴y与x的函数关系式为y=10x+300;
(2)设该款电子产品每天的销售利润为w元,
由题意得w=(x10)y
=(x10)(10x+300)
=10x2+400x3000
=10(x20)2+1000,
∵10<0,
∴当x=20时,w有最大值,w最大值为1000.
答:该款电子产品销售单价定为20元时,每天销售利润最大,最大销售利润为1000元;
(3)设捐款后每天剩余利润为z元,
由题意可得z=10x2+400x3000300=10x2+400x3300,
令z=450,即10x2+400x3300=450,
x240x+375=0,
解得x1=15,x2=25,
∵10<0,
∴当该款电子产品的销售单价每件不低于15元,且不高于25元时,可保证捐款后每天剩余利润不低于450元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
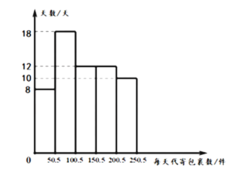
(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
重量G(单位:千克) |
|
|
|
件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
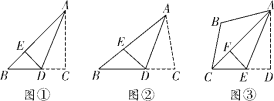
【题目】(1)操作发现
如图①,在![]() 中,
中,![]() ,点D是
,点D是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() ,使得点C恰好落在
,使得点C恰好落在![]() 上的点E处.则
上的点E处.则![]() 的数量关系为______;
的数量关系为______;![]() ________;
________;
(2)问题解决
如图②,若(1)中![]() ,其他条件不变,请猜想
,其他条件不变,请猜想![]() 之间的关系,并证明你的结论;
之间的关系,并证明你的结论;
(3)类比探究
如图③,在四边形![]() 中,
中,![]() ,连接
,连接![]() ,点E是
,点E是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() 使得点D正好落在
使得点D正好落在![]() 上的点F处,若
上的点F处,若![]() ,直接写出
,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象由函数
的图象由函数![]() 的图象平移得到,且经过点(1,2).
的图象平移得到,且经过点(1,2).
(1)求这个一次函数的解析式;
(2)当![]() 时,对于
时,对于![]() 的每一个值,函数
的每一个值,函数![]() 的值大于一次函数
的值大于一次函数![]() 的值,直接写出
的值,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年某中学举行的冬季阳径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
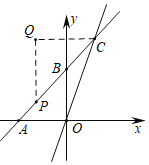
【题目】如图,在平面直角坐标系中,直线11:y=k1x+3分别与x轴,y轴交于A(﹣3,0),B两点,与直线l2:y=k2x交于点C,S△AOC=9.
(1)求tan∠BAO的值;
(2)求出直线l2的解析式;
(3)P为线段AC上一点(不含端点),连接OP,一动点H从点O出发,沿线段OP以每秒1个单位长度的速度运动到P,再沿线段PC以每秒![]() 个单位长度的速度运动到点C后停止,请直接写出点H在整个运动过程的最少用时.
个单位长度的速度运动到点C后停止,请直接写出点H在整个运动过程的最少用时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在一次打篮球时,篮球传出后的运动路线为如图所示的抛物线,以小明所站立的位置为原点O建立平面直角坐标系,篮球出手时在O点正上方1m处的点P.已知篮球运动时的高度y(m)与水平距离x(m)之间满足函数表达式y=-![]() x2+x+c.
x2+x+c.
(1)求y与x之间的函数表达式;
(2)球在运动的过程中离地面的最大高度;
(3)小亮手举过头顶,跳起后的最大高度为BC=2.5m,若小亮要在篮球下落过程中接到球,求小亮离小明的最短距离OB.

查看答案和解析>>
科目:初中数学 来源: 题型:
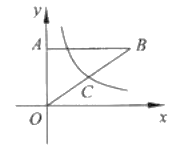
【题目】如图,在平面直角坐标系中,![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴的正半轴上,顶点
轴的正半轴上,顶点![]() 在第一象限,函数
在第一象限,函数![]() 的图象与边
的图象与边![]() 交于点
交于点![]() ,并且点
,并且点![]() 为边
为边![]() 的中点.若
的中点.若![]() 的面积为12,则
的面积为12,则![]() 的值为______.
的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com