[题目]解方程(1)(2)(3)(4) 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】解方程

(1)

(2)

(3)

(4)

【答案】（1）x1=4，x2=-2；（2）x=；（3）；（4）.

【解析】

（1）直接开平方即可；（2）两边同时除以8，开立方即可；（3）利用加减消元法先求出y的值，再代入求出x的值即可；（4）去分母得3x+2y=7，利用代入消元法求出x的值，进而求出y值即可.

（1）

x-1=±3

x1=4，x2=-2.

（2）

(x+2)3=

x+2=

x=.

（3）

②-①得3y=-3，

解得：y=-1，

把y=-1代入①得x=2，

∴原方程组的解为.

（4）

由②得3(x-1)+2(y+1)=6，

整理得：3x+2y=7③，

由①得：y=4-x，

把y=4-x代入③得：3x+8-2x=7，

解得：x=-1，

把x=-1代入①得y=5，

∴原方程组的解为.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图在平面直角坐标系中，A.B两点的坐标分别为（﹣2，2），（1，8），

（1）求△ABO的面积．

（2）若y轴上有一点M，且△MAB的面积为10．求M点的坐标．

（3）如图，把直线AB以每秒2个单位的速度向右平移，运动t秒钟后，直线AB过点F（0，﹣2），此时A点的坐标为　　，B点的坐标为　　，过点A作AE⊥y轴于点E，过点B作BD⊥y轴于点D，请根据S△FBD=S△FAE+S梯形ABDE，求出满足条件的运动时间t的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知a＝2019x+2018，b＝2019x+2019，c＝2019x+2020．则多项式a2+b2+c2﹣ab﹣bc﹣ac的值为（　　）

A. 1B. 2C. 3D. 4

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】二次函数y=ax +bx+c（a≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x=2，下列结论：①抛物线与x轴的另一个交点是（5，0）；②4a+c＞2b；③4a+b=0；④当x＞-1时，y的值随x值的增大而增大．其中正确的结论有（）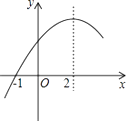

A.1个
B.2个
C.3个
D.4个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图(十九)，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依序为2、3、4、6，且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框，则任两螺丝的距离之最大值为何？

(A) 5 (B) 6 (C) 7 (D) 10

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为了提高产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场．现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两个工厂了解情况，获得如下信息：

信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；

信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍．

根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知，如图，抛物线与x轴交点坐标为A（1，0），C（-3，0），

（1）若已知顶点坐标D为（-1，4）或B点（0，3），选择适当方式求抛物线的解析式.
（2）若直线DH为抛物线的对称轴，在（1）的基础上，求线段DK的长度，并求△DBC的面积．
（3）将图（2）中的对称轴向左移动，交x轴于点p（m，0）(－3<m<－1)，与线段BC、抛物线的交点分别为点K、Q，用含m的代数式表示QK的长度，并求出当m为何值时，△BCQ的面积最大？