
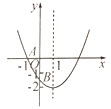
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的交点
轴的交点![]() 在
在![]() 和
和![]() 之间(不包括这两点),对称轴为直线
之间(不包括这两点),对称轴为直线![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是________.
.其中正确的是________.
【答案】①③④⑤
【解析】
①由抛物线的开口方向、对称轴以及与y轴的交点,可得出a>0、b<0、c<0,进而可得出abc>0,结论①正确;②由抛物线的对称轴及点A的坐标,可得出抛物线与x轴的另一交点坐标,结合抛物线的开口可得出当x=2时,y=4a+2b+c<0,结论②错误;③由a>0、b<0、c<0,可得出![]() ,结论③正确;④由当x=-1时y=a-b+c=0,结合b=-2a可得出3a=-c,再根据-2<c<-1,即可求出
,结论③正确;④由当x=-1时y=a-b+c=0,结合b=-2a可得出3a=-c,再根据-2<c<-1,即可求出![]() ,结论④正确;⑤由a-b+c=0、a>0,可得出-b+c<0,即b>c,结论⑤正确.综上即可得出结论.
,结论④正确;⑤由a-b+c=0、a>0,可得出-b+c<0,即b>c,结论⑤正确.综上即可得出结论.
①∵抛物线开口向上,对称轴为直线x=1,与y轴的交点在(0,2)和(0,1)之间,
∴a>0, ![]() ,2<c<1,
,2<c<1,
∴b<0,abc>0,结论①正确;
②∵抛物线与x轴交于点A(1,0),对称轴为直线x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∴当x=2时,y=4a+2b+c<0,结论②错误;
③∵a>0,b<0,c<0,
∴4ac<0, ![]() >0,
>0,
∴![]() ,结论③正确;
,结论③正确;
④当x=1时,y=ab+c=0,
∴ab=c.
∵b=2a,
∴3a=c.
又∵2<c<1,
∴![]() ,结论④正确;
,结论④正确;
⑤∵当x=1时,y=ab+c=0,a>0,
∴b+c<0,
∴b>c,结论⑤正确。
综上所述:正确的结论有①③④⑤.
故答案为:①③④⑤.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知函数y=﹣x2+bx+c(其中b,c是常数)
(1)四位同学在研究此函数时,甲发现当x=0时,y=5;乙发现函数的最大值为9;丙发现函数图象的对称轴是直线x=2;丁发现4是方程﹣x2+bx+c=0的一个根.已知这四位同学中只有一位发现的结论是错误的,请直接写出错误的那个人是谁,并求出此函数表达式;
(2)在(1)的条件下,函数y=﹣x2+bx+c的图象顶点为A,与x轴正半轴交点为B,与y轴的交点为C,若将该图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)若c=b2,当﹣2≤x≤0时,函数y=﹣x2+bx+c的最大值为5,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
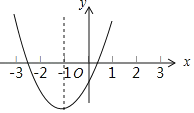
【题目】已知二次函数y=ax2+bx+c的图象如图,其对称轴x=﹣1,给出下列结果:①b2>4ac;②abc>0;③2a+b=0;④a﹣b+c<0;⑤3a+c>0.其中正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
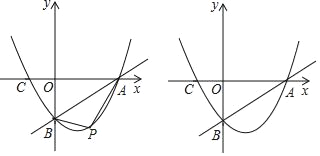
【题目】已知:直线y=![]() x﹣3与x轴、y轴分别交于点A、B,抛物线y=
x﹣3与x轴、y轴分别交于点A、B,抛物线y=![]() x2+bx+c经过点A、B,且交x轴于点C.
x2+bx+c经过点A、B,且交x轴于点C.
(1)求抛物线的解析式;
(2)点P为抛物线上一点,且点P在AB的下方,设点P的横坐标为m.
①试求当m为何值时,△PAB的面积最大;
②当△PAB的面积最大时,过点P作x轴的垂线PD,垂足为点D,问在直线PD上否存在点Q,使△QBC为直角三角形?若存在,直接写出符合条件的Q的坐标若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校门口竖着“前方学校,减速慢行”的交通指示牌CD,数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动,他们定好了如下测量方案:
项目 | 内容 |
课题 | 测量交通指示牌CD的高度 |
测量示意图 |
|
测量步骤 | (1)从交通指示牌下的点M处出发向前走10 米到达A处; (2)在点A处用量角仪测得∠DAM=27°; (3)从点A沿直线MA向前走10米到达B处;(4)在点B处用量角仪测得∠CBA=18°. |
请你帮助该小组同学根据上表中的测量数据,求出交通指示牌CD的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)
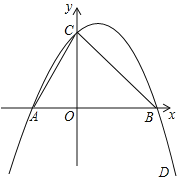
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若P是抛物线上一点,且S△ABP=![]() S△ABC,这样的点P有几个请直接写出它们的坐标.
S△ABC,这样的点P有几个请直接写出它们的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用黑白棋子摆出下列一组图形,根据规律可知.
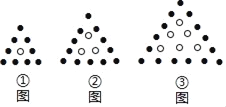
(1)在第n个图中,白棋共有 枚,黑棋共有 枚;
(2)在第几个图形中,白棋共有300枚;
(3)白棋的个数能否与黑棋的个数相等?若能,求出是第几个图形,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020春节期间,为了进一步做好新型冠状病毒感染的肺炎疫情防控工作,防止新型肺炎外传,切断传播途径.项城市市区各入口一些主要路段均设立了检测点,对出入人员进行登记和体温检测。下图为一关口的警示牌,已知立杆AB高度是3m,从侧面D点测得显示牌顶端C点和底端B点的仰角分别是60°和45°.求警示牌BC的高度.
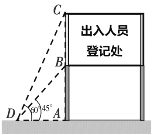
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B. 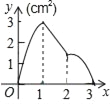 C.
C.  D.
D. 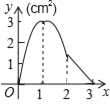
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com