
【题目】如图,已知BC=EC,∠BCE=∠ACD,如果只添加一个条件,使△ABC ≌ △DEC,则添加的条件不能为( )
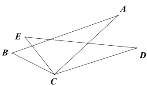
A. ∠B=∠E B. AC=DC C. ∠A=∠D D. AB=DE
【答案】D
【解析】
先求出∠ACB=∠DCE,全等三角形的判定定理有SAS,ASA,AAS,SSS,根据以上定理逐个判断即可.
∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
∴∠ACB=∠DCE,
A、∠B=∠E,BC=EC,∠ACB=∠DCE,符合全等三角形的判定定理ASA,能推出△ABC≌△DEC,故本选项错误;
B、AC=DC,∠ACB=∠DCE,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故本选项错误;
C、∠A=∠D,∠ACB=∠DCE,BC=EC,符合全等三角形的判定定理AAS,能推出△ABC≌△DEC,故本选项错误;
D、AB=DE,BC=EC,∠ACB=∠DCE,不符合全等三角形的判定定理,不能推出△ABC≌△DEC,故本选项正确;
故选D.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形的三角板如图1所示放置,图2是由它抽象出的几何图形,点B、C、E在同一条直线上,连结DC.
(1)求证:△ABE≌△ACD;
(2)判定BE和CD的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,等腰直角△ABC在平面直角坐标系中的位置如图,点A(0,a),点B(b,0),点C在第四象限,且满足a2+b2-4a+12b+40=0.

(1)求点C的坐标;
(2)若AC交x轴于M,BC交y轴于D,E是AC上一点,且CE=AM,连DM,求证:AD+DE=BM;
(3)在y轴上取点F(0,6),点H是y轴上F下方任一点,作HG⊥BH交射线CF于G,在点H位置变化的过程中,![]() 是否为定值,若是,求其值,若不是,说明理由.
是否为定值,若是,求其值,若不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
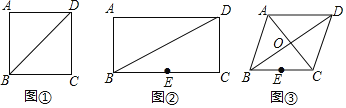
【题目】问题探究
![]() 请在图
请在图![]() 的正方形ABCD的对角线BD上作一点P,使
的正方形ABCD的对角线BD上作一点P,使![]() 最小;
最小;
![]() 如图
如图![]() ,点P为矩形ABCD的对角线BD上一动点,
,点P为矩形ABCD的对角线BD上一动点,![]() ,
,![]() ,点E为BC边的中点,请作一点P,使
,点E为BC边的中点,请作一点P,使![]() 最小,并求这个最小值;
最小,并求这个最小值;
问题解决
![]() 如图
如图![]() ,李师傅有一块边长为1000米的菱形采摘园ABCD,
,李师傅有一块边长为1000米的菱形采摘园ABCD,![]() 米,BD为小路,BC的中点E为一水池,李师傅现在准备在小路BD上建一个游客临时休息纳凉室P,为了节省土地,使休息纳凉室P到水池E与大门C的距离之和最短,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离;若不存在,请说明理由.
米,BD为小路,BC的中点E为一水池,李师傅现在准备在小路BD上建一个游客临时休息纳凉室P,为了节省土地,使休息纳凉室P到水池E与大门C的距离之和最短,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校七年级学生期末考试数学成绩情况,决定进行抽样分析已知该校七年级共有10个班,每班40名学生,请根据要求回答下列问题:
(1)若要从全年级学生中抽取一个40人的样本,你认为以下抽样方法中比较合理的有__________.(只要填写序号).
①随机抽取一个班级的学生;
②在全年级学生中随机抽取40名男学生;
③在全年级10个班中各随机抽取4名学生.
(2)将抽取的40名学生的数学成绩进行分组,并绘制频数表和成绩分布统计图(不完整),如图:
①请补充完整频数表;
成绩(分) | 频数 | 频率 |
| __________ | 0.3 |
| __________ | 0.4 |
| 8 | __________ |
| 4 | __________ |
②写出图中![]() 、
、![]() 类圆心角度数;并估计全年级
类圆心角度数;并估计全年级![]() 、
、![]() 类学生大约人数.
类学生大约人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
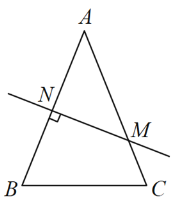
(1)若∠C =70°,求![]() 的度数;
的度数;
(2)若∠C =α,请用含α的式子表示![]() ;
;
(3)连接MB,若AB =8,BC =6.
①求△![]() 的周长;
的周长;
②在直线![]() 上是否存在点P,使(PB+CP)的值最小?若存在,标出点P的位置并求(PB+CP)的最小值;若不存在,说明理由.
上是否存在点P,使(PB+CP)的值最小?若存在,标出点P的位置并求(PB+CP)的最小值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC.

(1)如果∠B+∠C=120°,则∠AED的度数=______.(直接写出结果)
(2)根据⑴的结论,猜想∠B+∠C与∠AED之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com