

分析 先求得AC=BC然后利用解直接三角形的方法求出AC,再在Rt△AEC中解出AE的长,从而求出A到地面的高度为AE+2.
解答  解:由题可知:如图,BH⊥HE,AE⊥HE,CD=2,BC=4
解:由题可知:如图,BH⊥HE,AE⊥HE,CD=2,BC=4
∠BCH=30°,∠ABC=80°,∠ACE=70°
∵∠BCH+∠ACB+∠ACE=180°
∴∠ACB=80°
∵∠ABC=80°
∴∠ABC=∠ACB
∴AB=AC
过点A作AM⊥BC于M,
∴CM=BM=2
∵在Rt△ACM中,CM=2,∠ACB=80°
∴$\frac{CM}{AC}=cos$∠ACB=cos80°≈0.17
∴AC=$\frac{CM}{0.17}$=$\frac{200}{17}$
∵在Rt△ACE中,AC=$\frac{200}{17}$,∠ACE=70°
∴$\frac{AE}{AC}=sin$∠ACE=sin70°≈0.94
∴AE=$\frac{200}{17}$×0.94=$\frac{188}{17}$≈11.1
故可得点A到地面的距离为13.1米.
点评 本题考查了解直角三角形的应用,正确求得AE的长是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
 如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )
如图,在等腰△ABC中,直线l垂直底边BC,现将直线l沿线段BC从B点匀速平移至C点,直线l与△ABC的边相交于E、F两点.设线段EF的长度为y,平移时间为t,则下图中能较好反映y与t的函数关系的图象是( )| A. |  | B. |  | C. | 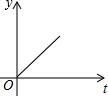 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某建筑物BC顶部有一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.
如图,某建筑物BC顶部有一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )| A. | 50$\sqrt{3}$ | B. | 51 | C. | 50$\sqrt{3}$+1 | D. | 101 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:
901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1,四边形EFQP的面积为S2,四边形PQCB的面积为S3.
如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q,记△AEF的面积为S1,四边形EFQP的面积为S2,四边形PQCB的面积为S3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一个几何体由大小相同的小方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状图是( )
一个几何体由大小相同的小方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,则从正面看到几何体的形状图是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com