
 如图,正方形ABCD的边长为4cm,动点P从点D开始沿着D→C→B的路线以1cm/s的速度移动,到达点B停止运动,设点P的运动时间为x s,解答下列问题:
如图,正方形ABCD的边长为4cm,动点P从点D开始沿着D→C→B的路线以1cm/s的速度移动,到达点B停止运动,设点P的运动时间为x s,解答下列问题:分析 (1)根据正方形ABCD的边长为4cm,当x=1时,动点P在边DC上,根据三角形的面积即可得到结论;当x=5时,动点P在边BC上,于是得到结论;
(2)当点P在DC边上运动时,当点P在CB边上运动时,根据三角形的面积公式即可得到结论.
解答 解: (1)∵正方形ABCD的边长为4cm,当x=1时,动点P在边DC上,
(1)∵正方形ABCD的边长为4cm,当x=1时,动点P在边DC上,
∴△APC的面积为=$\frac{1}{2}$AD•P=$\frac{1}{2}×4×(4-1)$=6cm2;
当x=5时,动点P在边BC上,
∴△APC的面积=$\frac{1}{2}$AB•CP=$\frac{1}{2}×4×(5-4)$=2cm2;
故答案为:6,2;
(2)当点P在DC边上运动时,△APC的面积=$\frac{1}{2}$AD•PC=$\frac{1}{2}×4×(4-x)$=(-2x+8)cm2,
当点P在CB边上运动时,△APC的面积=$\frac{1}{2}$AD•CP=$\frac{1}{2}×4×(x-4)$=(2x-8)cm2.
故答案为:-2x+8,2x-8.
点评 本题考查了正方形的性质,三角形的面积,熟练掌握正方形的性质是解题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
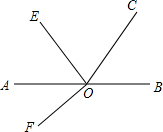 已知O为直线AB上一点,∠BOC=50°,锐角∠AOE在∠A0C内部.如图,过O作OF,使∠EOF为直角,若锐角∠AOE大小变化时,下面两个结论:①∠EOC-∠AOF的值不变;②∠EOC+∠AOF的值不变.其中只有一个正确,请选择正确的结论并说明理由,求出其值.
已知O为直线AB上一点,∠BOC=50°,锐角∠AOE在∠A0C内部.如图,过O作OF,使∠EOF为直角,若锐角∠AOE大小变化时,下面两个结论:①∠EOC-∠AOF的值不变;②∠EOC+∠AOF的值不变.其中只有一个正确,请选择正确的结论并说明理由,求出其值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
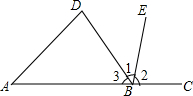 如图,
如图,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
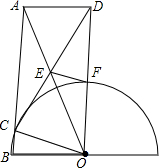 如图.在△AB0中,AB=A0=2B0,以O为圆心,OB为半径的半圆交AB边于点C.△ABO绕点O顺时针旋转得△DCO,DC交AO于点E,DO交半圆于点F,连接AD,EF.
如图.在△AB0中,AB=A0=2B0,以O为圆心,OB为半径的半圆交AB边于点C.△ABO绕点O顺时针旋转得△DCO,DC交AO于点E,DO交半圆于点F,连接AD,EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y千米,y关于x的函数关系如图所示.
设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回,设x秒后两车间的距离为y千米,y关于x的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com