
����Ŀ�����ⷢ�֣���ͼ1������ABC�У���C=90�����ֱ���AC��BCΪ���������������ACDE��������BCFG��
��1����ABC����DCF����Ĺ�ϵ��______________�������ں�������д�������������������
��2����չ̽��������C��90������1���еĽ��ۻ�������������������ͼ2����֤����������������˵�����ɣ�
��3��������⣺��ͼ3�����ı���ABCD�У�AC��BD����AC��BD�ĺ�Ϊ10���ֱ����ı���ABCD��������Ϊ���������������ABFE��������BCHG��������CDJI��������DALK�����ã�2���Ľ��ۣ�ͼ����Ӱ���ֵ�������Ƿ������ֵ������У���������ֵ�����û�У���˵�����ɣ�
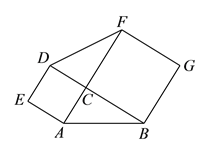
ͼ1
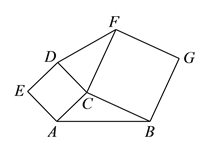
ͼ2
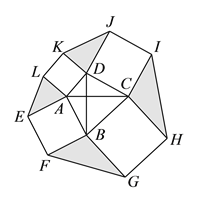
ͼ3
���𰸡���1����ȣ���2�����������ɼ���������3����Ӱ���ֵ�����������ֵ,���ֵΪ25
���������⣺��1����ȣ�
��2���������������£�
��ͼ���ӳ�BC����P������A��AP��BP�ڵ�P������D��DQ��FC�ڵ�Q��
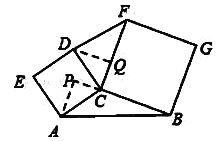
���APC=��DQC=90�㣮
���ı���ACDE���ı���BCFG��Ϊ�����Σ�
��AC=CD��BC=CF����ACP+��PCD=90�㣬��DCQ+��PCD=90�㣬
���ACP=��DCQ��
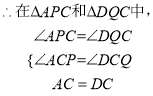
���APC�ա�DQC��AAS����
��AP=DQ��
�֡�S��ABC=![]() BCAP��S��DFC =
BCAP��S��DFC =![]() FCDQ��
FCDQ��
��S��ABC=S��DFC.
��3��ͼ����Ӱ���ֵ�����������ֵ
���ɣ��ɣ�2���Ľ��ۿ�֪��
![]()
![]()
��AC=m,��BD=10-m, ��AC��BD.
��![]() .
.
��![]()
����Ӱ���ֵ�����������ֵ,���ֵΪ25


 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д� ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и��鵥��ʽ��ͬ������ǣ�������
A. 4x��4y B. xy2��4xy C. 4xy2�ͩ�x2y D. ��4xy2��y2x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���A����ʾ��ʵ��Ϊ2����B����ʾ��ʵ��Ϊa����A�İ뾶Ϊ3������B�ڡ�A�⣬��a��ֵ�����ǣ�������
A.��1B.0C.5D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB=AC��CD��AB�ڵ�D��BE��AC�ڵ�E��BE��CD�ཻ�ڵ�O�� 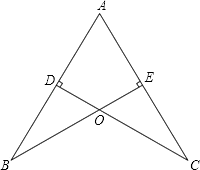
��1����֤��AD=AE��
��2���Բ��룺OA��BC��λ�ù�ϵ��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���A(2��0)����B (0��1)������A��ֱ��l��ֱ���߶�AB����P��ֱ��l��һ���㣬����P��PC��x�ᣬ����ΪC������ACP��AP����![]() ��ʹ��C���ڵ�D��������A��D��PΪ���������������ABP���ƣ�����������������ĵ�P������Ϊ___________________________��
��ʹ��C���ڵ�D��������A��D��PΪ���������������ABP���ƣ�����������������ĵ�P������Ϊ___________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
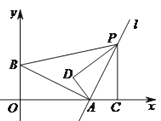
����Ŀ����ͼ���������ĸ���������BC=B��C����AC=A��C���ۡ�A��CA=��B��CB����AB=A��B���У���ȡ����Ϊ���������µ�һ��Ϊ���ۣ��������Թ�����ȷ�Ľ��۵ĸ����ǣ� �� 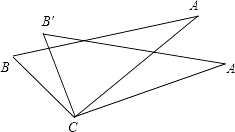
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=30�㣬��M��N�ֱ�������OA��OB�ϵĶ��㣬OPƽ�֡�AOB����OP=6����PMN���ܳ���СֵΪ �� 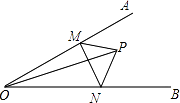
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=x2+bx+c��x�ύ��A��B���㣬B������Ϊ��3��0������y�ύ�ڵ�C��0����3��
��1���������ߵĽ���ʽ��
��2����P��������λ�ڵ������IJ������˶������ı���ABPC��������ʱ�����P��������ı���ABPC����������
��3��ֱ��l����A��C���㣬��Q��������λ��y�����IJ������˶���ֱ��m������B�͵�Q���Ƿ����ֱ��m��ʹ��ֱ��l��m��x��Χ�ɵ������κ�ֱ��l��m��y��Χ�ɵ����������ƣ������ڣ����ֱ��m�Ľ���ʽ���������ڣ���˵�����ɣ�
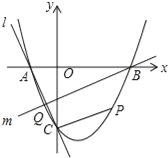
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AC=BC����ACB=90�㣬��D��AB���е㣬��E��AB����һ�㣮
��1��ֱ��BF��ֱ��CE�ڵ�F����CD�ڵ�G����ͼl������֤��AE=CG�� 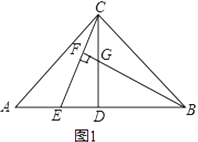
��2��ֱ��AH��ֱ��CE������ΪH����CD���ӳ����ڵ�M����ͼ2�����ҳ�ͼ����BE��ȵ��߶Σ�����Ҫ���Ӹ����ߣ�����˵�����ɣ� 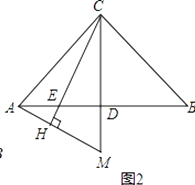
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com