
【题目】(本题10分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,![]() =
=![]() 时,求DE的长.
时,求DE的长.
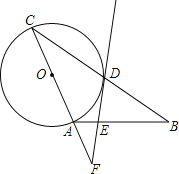
【答案】(1)见解析(2)![]() .
.
【解析】试题分析:(1)连接OD .根据EF与⊙O相切.可得OD⊥EF,所以要证明FE⊥AB,只要证明OD∥AB即可;
(2)首先利用sin∠CFD=![]() ,在Rt△AEF中,求出AF的长,然后利用△ODF∽△AEF.求出圆的半径,再根据EB=AB-AE计算即可.
,在Rt△AEF中,求出AF的长,然后利用△ODF∽△AEF.求出圆的半径,再根据EB=AB-AE计算即可.
试题解析:(1)证明:连接OD . (如图)
∵ OC=OD,
∴ ∠OCD="∠ODC."
∵ AB=AC,
∴∠ACB=∠B.
∴ ∠ODC=∠B.
∴ OD∥AB. 1分
∴ ∠ODF =∠AEF.
∵ EF与⊙O相切.
∴ OD⊥EF,∴ ∠ODF =90°.
∴∠AEF ="∠ODF" =90°.
∴ EF⊥AB. 2分
(2)解:由(1)知:OD∥AB,OD⊥EF .
在Rt△AEF中,sin∠CFD =![]() =
=![]() ,AE=6.
,AE=6.
∴ AF=10. 3分
∵ OD∥AB,
∴ △ODF∽△AEF.
∴![]() .
.
∴![]() .
.
解得r=![]() . 4分
. 4分
![]() ∴ AB=" AC=2r" =
∴ AB=" AC=2r" =![]() .
.
∴ EB=AB-AE=![]() -6=
-6=![]() . 5分
. 5分


科目:初中数学 来源: 题型:
【题目】四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
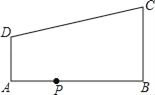
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
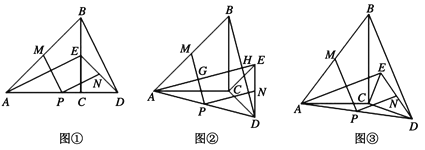
【题目】如图①,△ABC与△CDE是等腰直角三角形,直角边AC、CD在同一条直线上,点M、N分别是斜边AB、DE的中点,点P为AD的中点,连接AE、BD.
(1)请直接写出PM与PN的数量关系及位置关系 ;
(2)现将图①中的△CDE绕着点C顺时针旋转α(0°<α<90°),得到图②,AE与MP、BD分别交于点G、H.请直接写出PM与PN的数量关系及位置关系 ;
(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
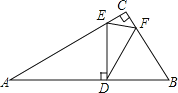
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE是圆O的直径,点B在AE的延长线上,点D在圆O上,且AC⊥DC, AD平分∠EAC
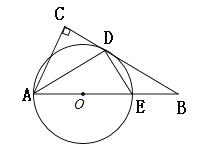
(1)求证:BC是圆O的切线。
(2)若BE=8,BD=12,求圆O的半径,
查看答案和解析>>
科目:初中数学 来源: 题型:
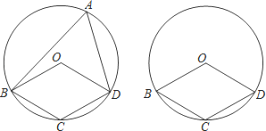
【题目】如图,四边形OBCD中的三个顶点在⊙O上,点A是⊙O上的一个动点(不与点B、C、D重合).
(1)若点A在优弧![]() 上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
上,且圆心O在∠BAD的内部,已知∠BOD=120°,则∠OBA+∠ODA= °.
(2)若四边形OBCD为平行四边形.
①当圆心O在∠BAD的内部时,求∠OBA+∠ODA的度数;
②当圆心O在∠BAD的外部时,请画出图形并直接写出∠OBA与∠ODA的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P,Q为平面直角坐标系xOy中不重合的两点,以点P为圆心且经过点Q作⊙P,则称点Q为⊙P的“关联点”,⊙P为点Q的“关联圆”.
(1)已知⊙O的半径为1,在点E(1,1),F(﹣![]() ,
,![]() ),M(0,-1)中,⊙O的“关联点”为______;
),M(0,-1)中,⊙O的“关联点”为______;
(2)若点P(2,0),点Q(3,n),⊙Q为点P的“关联圆”,且⊙Q的半径为![]() ,求n的值;
,求n的值;
(3)已知点D(0,2),点H(m,2),⊙D是点H的“关联圆”,直线y=﹣![]() x+4与x轴,y轴分别交于点A,B.若线段AB上存在⊙D的“关联点”,求m的取值范围.
x+4与x轴,y轴分别交于点A,B.若线段AB上存在⊙D的“关联点”,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为K90的化学赛道,其中助滑坡AB长90米,坡角a=40°,一个曲面平台BCD连接了助滑坡AB与着陆坡,某运动员在C点飞向空中,几秒之后落在着陆坡上的E处,已知着陆坡DE的坡度i=1: ![]() ,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)
,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)

A. 101.4 B. 101.3 C. 100.4 D. 100.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com