
定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足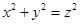 ,则称这个三角形为勾股三角形.
,则称这个三角形为勾股三角形.
(1)已知某一勾股三角形的三个内角度数从小到大依次为x°、y°和z°,且xy=2160,求x+y的值;
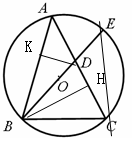
(2)如图,△ABC是⊙O的内接三角形,AB=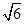 ,AC=
,AC=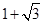 ,BC=2,BE是⊙O的直径,交AC于D.
,BC=2,BE是⊙O的直径,交AC于D. 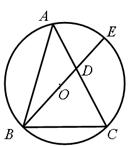
①求证:△ABC是勾股三角形;
②求DE的长.
(1)102;(2)①过B作BH⊥AC于H,设AH=x,则CH=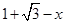 ,在Rt△ABH和Rt△CBH中,根据勾股定理即可求得
,在Rt△ABH和Rt△CBH中,根据勾股定理即可求得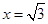 ,所以
,所以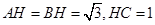 ,则可得
,则可得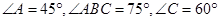 ,再根据勾股定理的逆定理即可证得结论;②
,再根据勾股定理的逆定理即可证得结论;②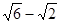
解析试题分析:(1)由三角形的内角和、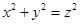 、xy=2160可得关于x、y、z的方程组,即可求得结果;
、xy=2160可得关于x、y、z的方程组,即可求得结果;
(2)①过B作BH⊥AC于H,设AH=x,则CH=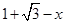 ,在Rt△ABH和Rt△CBH中,根据勾股定理即可求得
,在Rt△ABH和Rt△CBH中,根据勾股定理即可求得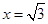 ,所以
,所以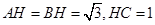 ,则可得
,则可得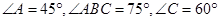 ,再根据勾股定理的逆定理即可证得结论;②连接CE,则
,再根据勾股定理的逆定理即可证得结论;②连接CE,则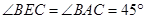 ,再根据圆周角定理可得
,再根据圆周角定理可得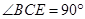 ,即得BC=CE=2,
,即得BC=CE=2,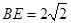 ,过D作DK⊥AB于K,设KD=h,则
,过D作DK⊥AB于K,设KD=h,则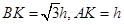 ,由
,由 ,即可求得结果.
,即可求得结果.
(1)由题意可得: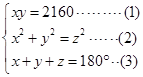
由(3)得: 代入(2)得:
代入(2)得: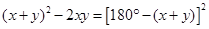
把(1)代入得: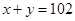
(2)①过B作BH⊥AC于H,设AH=x,则CH=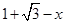 ,
,
Rt△ABH中,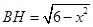 ,Rt△CBH中,
,Rt△CBH中,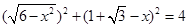
解得: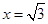 所以,
所以,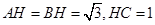
所以,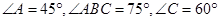
因为,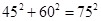 所以,△ABC是勾股三角形
所以,△ABC是勾股三角形
②连接CE,则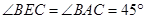 ,又BE是直径,所以,
,又BE是直径,所以,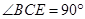
所以,BC=CE=2,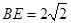
过D作DK⊥AB于K,设KD=h,则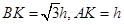
由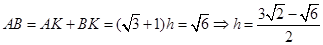
所以,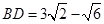
所以,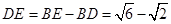 .
.
考点:圆的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
 (2007•东城区一模)我们给出如下定义:如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c.
(2007•东城区一模)我们给出如下定义:如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c.查看答案和解析>>
科目:初中数学 来源: 题型:
 学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.| 6 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2014届浙江温州市八年级第二学期开学考试数学试卷(解析版) 题型:解答题
定义:对于任意的三角形,设其三个内角的度数分别为x°、y°和z°,若满足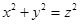 ,则称这个三角形为勾股三角形.
,则称这个三角形为勾股三角形.
(1)已知某一勾股三角形的三个内角度数从小到大依次为x°、y°和z°,且xy=2160,求x+y的值;
(2)如图,△ABC是⊙O的内接三角形,AB=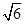 ,AC=
,AC=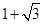 ,BC=2,BE是⊙O的直径,交AC于D.
,BC=2,BE是⊙O的直径,交AC于D.
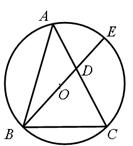
①求证:△ABC是勾股三角形;
②求DE的长.
查看答案和解析>>
科目:初中数学 来源:2007年北京市东城区中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com