
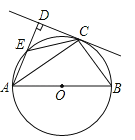
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
(1)求证:CE=CB;
(2)若AC=![]() ,CE=
,CE=![]() ,求AE的长.
,求AE的长.
【答案】(1)证明见解析;(2)3.
【解析】
试题分析:(1)连接OC,利用切线的性质和已知条件推知OC∥AD,根据平行线的性质和等角对等边证得结论;
(2)AE=AD﹣ED,通过相似三角形△ADC∽△ACB的对应边成比例求得AD=4,DC=2.在直角△DCE中,由勾股定理得到DE=![]() =1,故AE=AD﹣ED=3.
=1,故AE=AD﹣ED=3.
试题解析:(1)证明:连接OC,∵CD是⊙O的切线,∴OC⊥CD.
∵AD⊥CD,∴OC∥AD,∴∠1=∠3.
又OA=OC,∴∠2=∠3,∴∠1=∠2,∴CE=CB;
(2)解:∵AB是直径,∴∠ACB=90°,∵AC=![]() ,CB=CE=
,CB=CE=![]() ,∴AB=
,∴AB=![]() =
=![]() =5.∵∠ADC=∠ACB=90°,∠1=∠2,∴△ADC∽△ACB,∴
=5.∵∠ADC=∠ACB=90°,∠1=∠2,∴△ADC∽△ACB,∴![]() ,即
,即![]() ,∴AD=4,DC=2.在直角△DCE中,DE=
,∴AD=4,DC=2.在直角△DCE中,DE=![]() =1,∴AE=AD﹣ED=4﹣1=3.
=1,∴AE=AD﹣ED=4﹣1=3.



 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】如图12,已知抛物线![]() 过点
过点![]() ,
,![]() ,过定点
,过定点![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在抛物线上运动时,判断线段
在抛物线上运动时,判断线段![]() 与
与![]() 的数量关系(
的数量关系(![]() 、
、![]() 、
、![]() ),并证明你的判断;
),并证明你的判断;
(3)![]() 为
为![]() 轴上一点,以
轴上一点,以![]() 为顶点的四边形是菱形,设点
为顶点的四边形是菱形,设点![]() ,求自然数
,求自然数![]() 的值;
的值;
(4)若![]() ,在直线
,在直线![]() 下方的抛物线上是否存在点
下方的抛物线上是否存在点![]() ,使得
,使得![]() 的面积最大,若存在,求出点
的面积最大,若存在,求出点![]() 的坐标及
的坐标及![]() 的最大面积,若不存在,请说明理由.
的最大面积,若不存在,请说明理由. 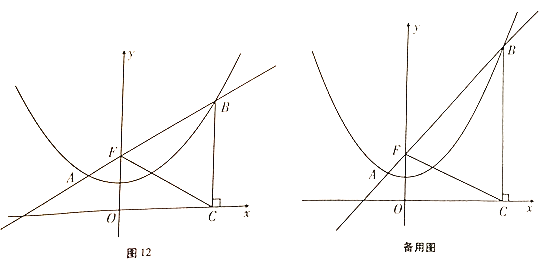
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形两条对角线长为6和8,菱形的边长为a,面积为S,则下列正确的是( )
A.a=5,S=24
B.a=5,S=48
C.a=6,S=24
D.a=8,S=48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系,折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题: 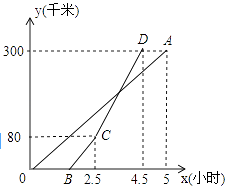
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
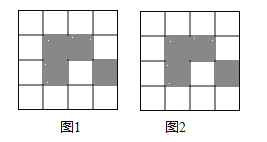
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陆地上最高处是珠穆朗玛峰顶,高出海平面8844m,记为+8844m;陆地上最低处是地处亚洲西部的死海,低于海平面约415m,记为( )
A.+415m
B.﹣415m
C.±415m
D.﹣8848m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店在防治新冠病毒期间,市场上抗病毒用品紧缺的情况下,将某药品提价100%,物价部门查处后,限定其提价幅度只能是原价的14%,则该药品现在降价的幅度是( )
A.43%B.45%C.57%D.55%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点![]() 沿
沿![]() 轴向左平移
轴向左平移![]() 个单位长度得到点
个单位长度得到点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交反比例函数
轴的平行线交反比例函数![]() 的图象于点
的图象于点![]() ,
,![]() .
.
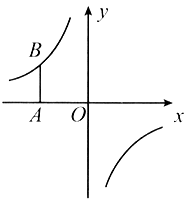
(1)求反比例函数的解析式;
(2)若![]() 、
、![]() 是该反比例函数图象上的两点,且
是该反比例函数图象上的两点,且![]() 时,
时,![]() ,指出点
,指出点![]() 、
、![]() 各位于哪个象限?并简要说明理由.
各位于哪个象限?并简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com