
分析 根据非负数的性质得出方程,再把a,b,c的值代入进行计算即可.
解答 解:∵(a-2b+1)2+$\sqrt{b-3}$=0,
∴$\left\{\begin{array}{l}{a-2b=-1}\\{b-3=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=5}\\{b=3}\end{array}\right.$,
∵$\root{3}{c}$=4,
∴c=64,
∴$\root{3}{{a}^{3}+{b}^{3}+c}$=$\root{3}{125+27+64}$=$\root{3}{216}$=6.
点评 本题考查了立方根、非负数的性质,掌握非负数的性质是解题的关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:填空题
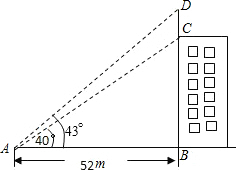 如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)
如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
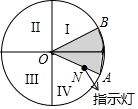 如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )
如图所示,将一个圆盘四等分,并把四个区域分别标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,只有区域Ⅰ为感应区域,中心角为55°的扇形AOB绕点0转动,在其半径OA上装有带指示灯的感应装置,当扇形AOB与区域I有重叠(原点除外)的部分时,指示灯会发光,否则不发光,当扇形AOB任意转动时,指示灯发光的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{7}{12}$ | C. | $\frac{5}{12}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查全国中学生心理健康现状 | B. | 调查你所在的班级同学的身高情况 | ||
| C. | 调查大东海食品合格情况 | D. | 调查交通法规普及情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
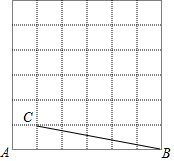 如图,是由边长相等的小正方形组成的网格,点A,B,C均在格点上,连接BC.
如图,是由边长相等的小正方形组成的网格,点A,B,C均在格点上,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
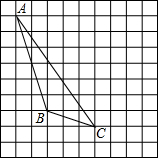 如图,在方格纸内将△ABC水平向右平移4个单位,再向下后平移1得到△A′B′C′.
如图,在方格纸内将△ABC水平向右平移4个单位,再向下后平移1得到△A′B′C′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com