Question

7．某市游泳馆为了满足不同顾客的需求，设计了三种游泳票：普通票价每次20元/张；金卡售价800元/张，每次凭卡不再收费；银卡售价200元/张，每次凭卡另收10元．这样顾客可根据游泳次数的多少选择不同的消费方式．普通票全年正常出售，两种优惠卡仅限暑期使用，不限次数．设游泳x次时，所需总费用为y元．
（1）分别写出选择银卡、普通票消费时，y与x之间的函数关系式；
（2）在同一个坐标系中，若三种消费方式对应的函数图象如图所示，请说出银卡消费和普通票消费对应的图象，并求出点A、B、C的坐标；
（3）请根据函数图象，直接写出选择哪种消费方式更合算．

Answer 1

分析 （1）银卡消费总费用=10×游泳次数+200（普通消费总费用=20×游泳次数），即可得出选择银卡、普通票消费时，y与x之间的函数关系式；
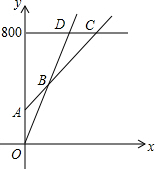
（2）根据函数关系式结合函数图象可得出：射线AC为银卡消费对应的图象，射线OD为普通票消费对应的图象．利用一次函数图象上点的坐标特征可得出点A、C的坐标，联立射线AC、OD的关系式成方程组，通过解方程组可求出点B的坐标；
（3）观察函数图象的上下位置关系结合点B、C的坐标，即可得出结论．

解答 解：（1）根据题意得：选择银卡消费时，y与x之间的函数关系式为y=10x+200；
选择普通票消费时，y与x之间的函数关系式为y=20x．
（2）射线AC为银卡消费对应的图象，射线OD为普通票消费对应的图象．
当x=0时，y=10x+200=200，
∴点A的坐标为（0，200）；
联立射线AC、OD的关系式成方程组，
$\left\{\begin{array}{l}{y=10x+200}\\{y=20x}\end{array}\right.$，解得：$\left\{\begin{array}{l}{x=20}\\{y=400}\end{array}\right.$，
∴点B的坐标为（20，400）；
当y=10x+200=800时，x=60，
∴点C的坐标为（60，800）．
（3）观察函数图象可知：当0≤x＜20时，选择普通消费更划算；当x=20时，选择银卡消费和普通消费费用相同；当20＜x＜60时，选择银卡消费更划算；当x=60时，选择银卡消费和金卡消费费用相同；当x＞60时，选择金卡消费更划算．

点评 本题考查了一次函数的应用、一次函数的图象以及一次函数图象上点的坐标特征，解题的关键是：（1）根据数量关系，找出函数关系式；（2）根据一次函数图象上点的坐标特征以及联立函数解析式成方程组，找出点A、B、C的坐标；（3）根据函数图象的上下位置关系找出结论．