
分析 (1)首先对括号内的整式利用多项式的乘法法则以及单项式与多项式的乘法法则计算化简,然后计算除法即可化简,最后代入数值计算即可;
(2)首先利用单项式与多项式的乘法法则以及完全平方公式计算,再合并同类项即可化简,最后代入数值计算即可.
解答 解:(1)原式=[5m2+20mn-3mn-12n2-5m2-20mn]÷3n
=[-3mn-12n2]÷3n
=-m-4n.
当m=2,n=-1时,原式=-2-4÷(-1)=2;
(2)原式=2a2+2ab-a2-2ab-b2
=a2-b2.
当a=3,b=5时,原式=32-52=-16.
点评 本题考查了整式的化简求值,正确理解多项式的乘法法则、以及乘法公式是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
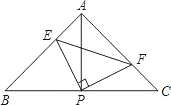 已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下结论:
已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下结论:| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
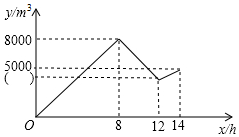 某企业一地下仓库发生渗水事故,凌晨0点开始渗漏,工作人员发现后于8点开始使用4台相同的抽水机排水,4小时后由于电路出现故障,为保证安全,有3台抽水机停止工作,2小时后电路故障仍然未完全排除,仅有两台抽水机恢复了工作,假设每小时的渗水量相同,仓库中的剩余水量不超过1000m3时才能对渗漏处进行封堵,仓库中存水量y(单位:m3)关于漏水时间x(单位:h)的函数图象如图所示.
某企业一地下仓库发生渗水事故,凌晨0点开始渗漏,工作人员发现后于8点开始使用4台相同的抽水机排水,4小时后由于电路出现故障,为保证安全,有3台抽水机停止工作,2小时后电路故障仍然未完全排除,仅有两台抽水机恢复了工作,假设每小时的渗水量相同,仓库中的剩余水量不超过1000m3时才能对渗漏处进行封堵,仓库中存水量y(单位:m3)关于漏水时间x(单位:h)的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com