
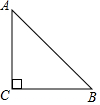
 如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长.
如图,△ABC中,∠C=90°,CA=CB=1,将△ABC绕点B顺时针旋转45°,得到△DBE(A、D两点为对应点),画出旋转后的图形,并求出线段AE的长. 分析 在BA上截取BE=BC,过点B作DB⊥BC,且DB=AB,则连接DE得到△DBE,再利用等腰三角形的性质得到∠ABC=45°,AB=$\sqrt{2}$BC=$\sqrt{2}$,利用旋转的性质得到∠CBE=45°,BC=BE=1,于是可判断点E在AB上,所以AE=AB-BE=$\sqrt{2}$-1.
解答 解:如图,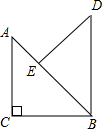
∵∠C=90°,CA=CB=1,
∴∠ABC=45°,AB=$\sqrt{2}$BC=$\sqrt{2}$,
∵△ABC绕点B顺时针旋转45°,得到△DBE,
∴∠CBE=45°,BC=BE=1,
∵∠CBE=∠CBA,
∴点E在AB上,
∴AE=AB-BE=$\sqrt{2}$-1.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了等腰直角三角形的性质.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
 如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡脚为45°的上坡向上走到C处,这时,PC=20$\sqrt{2}$m,点C与点A在同一水平线上,A、B、P、C在同一平面内.
如图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡脚为45°的上坡向上走到C处,这时,PC=20$\sqrt{2}$m,点C与点A在同一水平线上,A、B、P、C在同一平面内.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
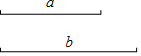 已知:线段a,b.
已知:线段a,b.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
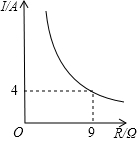 已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.
在平面直角坐标系中,对于任意一点P(x,y),我们做以下规定:d(P)=|x|+|y|,称d(P)为点P的坐标距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com