练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，在正方形ABCD中，点E，F在对角线BD上，若再添加一个条件，就可证出AE=CF．
    （1）你添加的条件是BE=DF．
    （2）请你根据题目中的条件和你添加的条件证明AE=CF．

    分析 （1）BE=DF（答案不唯一）；
    （2）根据SAS即可证明△ABE≌△CDF可得AE=CF．

    解答 解：（1）BE=DF（答案不唯一）．

    （2）证明：∵四边形ABCD是正方形，
    ∴AB∥CD，AB=CD，
    ∴∠ABD=∠BDC，
    又∵BE=DF（添加），
    ∴△ABE≌△CDF，
    ∴AE=CF．

    点评 本题考查正方形的性质、全等三角形的判定和性质等知识，解题的关键是熟练掌握全等三角形的判定方法，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．对于抛物线y=-$\frac{1}{2}$（x-1）2+3，下列说法正确的是（　　）
    A．开口向下，顶点坐标（1，3）B．开口向上，顶点坐标（3，-1）
    C．开口向下，顶点坐标（-1，3）D．开口向上，顶点坐标（-3，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．若（a-2）2+|b+3|=0，则（a+b）2017=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．设函数y=$\frac{1}{x}$与y=2x+1的图象的交点坐标为（a，b），求$\frac{1}{a}$-$\frac{2}{b}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．一次函数y=-3x+5图象上有两点A（$\frac{2}{3}$，y1）、B（2，y2），则y1与y2的大小关系是（　　）
    A．y1＞y2B．y1＜y2C．y1=y2D．y1≤y2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

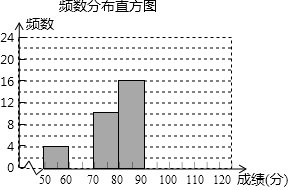    19．2017年3月在北京市召开的第十二届全国人民代表大会第五次会议上，环境问题再次成为大家讨论的重点内容之一．2017年6月5日是世界环境日，为纪念第46个世界环境日，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛，为了了解本次竞赛成绩情况，从中抽取了50名学生的成绩进行统计分析，经分组整理后绘制成频数分布表和频数分布直方图．
    频数分布表                            
    分组/分频数频率
    50～6040.08
    60～70a0.16
    70～80100.20
    80～90160.32
    90～100bc
    合计501
    （1）请你根据图表提供的信息，解答下列问题：a=8，b=12，c= 0.24；
    （2）请补全频数分布直方图；
    （3）若成绩在90分以上（含90分）为优秀，则该校成绩优秀的约为216人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．阅读下面的文字，解答问题：
    大家知道$\sqrt{2}$是无理数，而无理数是无限不循环小数，因此$\sqrt{2}$的小数部分我们不可能全部地写出来，于是小明用$\sqrt{2}$-1来表示$\sqrt{2}$的小数部分，你同意小明的表示方法吗？
    事实上，小明的表示方法是有道理的，因为$\sqrt{2}$的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵$\sqrt{4}$＜$\sqrt{7}$＜$\sqrt{9}$，即2＜$\sqrt{7}$＜3，∴$\sqrt{7}$的整数部分为2，小数部分为（$\sqrt{7}$-2）．
    根据以上提示回答下列问题：
    （1）如果$\sqrt{5}$的小数部分为a，$\sqrt{13}$的整数部分为b，求（a-b）2-b（a+1）的立方根；
    （2）若-$\sqrt{5}$=x+y，其中x是整数，且0＜y＜1，求x、y的值；
    （3）在（1）（2）的条件下求（x-a）（1-b+y）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．直线y=-$\frac{1}{2}$x+2分别交x轴、y轴于A、B两点，点0为坐标原点，则S△AOB=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．本题两小题
    （1）9$\sqrt{3}$+7$\sqrt{12}$-5$\sqrt{48}$+2$\sqrt{\frac{1}{3}}$
    （2）$\sqrt{48}$÷$\sqrt{3}$-2$\sqrt{\frac{1}{5}}$×$\sqrt{30}$+（2$\sqrt{2}$+$\sqrt{3}$）

    查看答案和解析>>

    同步练习册答案