
【题目】如图,△ABC 是等边三角形,点 D、E 分别在 BC、AC 上,且 BD=![]() BC,CE=
BC,CE= ![]() AC,BE、AD 相交于点 F,连接 DE, 则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DFDA;④AFBE=AEAC,正确的结论有( )
AC,BE、AD 相交于点 F,连接 DE, 则下列结论:①∠AFE=60°;②DE⊥AC;③CE2=DFDA;④AFBE=AEAC,正确的结论有( )
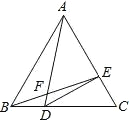
A.①②③B.①②④C.①③④D.①②③④
【答案】D
【解析】
本题是开放题,对结论进行一一论证,从而得到答案.
①利用△ABD≌△BCE,再用三角形的一个外角等于与它不相邻的两个内角和, 即可证∠AFE=60°;②从 CD 上截取 CM=CE,连接 E M,证△CEM 是等边三角形,可证明 DE⊥AC;
③△BDF∽△ADB,由相似比则可得到CE2=DFDA;
④只要证明了△AFE∽△BAE,即可推断出 AFBE=AEAC.
解:∵△ABC 是等边三角形
∴AB=BC=AC,∠BAC=∠ABC=∠BCA=60°
∵BD=![]() BC,CE=
BC,CE=![]() AC
AC
∴BD=EC
∴△ABD≌△BCE
∴∠BAD=∠CBE,
∵∠ABE+∠EBD=60°
∴∠ABE+∠CBE=60°
∵∠AFE 是△ABF 的外角
∴∠AFE=60°
∴①是对的;
如图,从 CD 上截取 CM=CE,连接 EM,则△CEM 是等边三角形
∴EM=CM=EC
∵EC=![]() CD
CD
∴EM=CM=DM
∴∠CED=90°
∴DE⊥AC,
∴②是对的;
由前面的推断知△BDF∽△ADB
∴BD:AD=DF:DB
∴BD2=DFDA
∴CE2=DFDA
∴③是对的;
在△AFE 和△BAE 中,∠BAE=∠AFE=60°,∠AEB 是公共角
∴△AFE∽△BAE
∴AFBE=AEAC∴④是正确的. 故选D.


科目:初中数学 来源: 题型:
【题目】一个四边形被一条对角线分割成两个三角形,如果被分割的两个三角形相似,我们被称为该对角线为相似对角线.
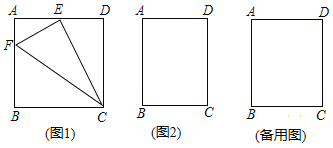
(1)如图1,正方形![]() 的边长为4,E为
的边长为4,E为![]() 的中点,
的中点,![]() ,连结
,连结![]() .
.![]() ,求证:
,求证:![]() 为四边形
为四边形![]() 的相似对角线.
的相似对角线.
(2)在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() ,且
,且![]() 是四边形
是四边形![]() 的相似对角线,求
的相似对角线,求![]() 的长.
的长.
(3)如图2,在矩形![]() 中,
中,![]() ,
,![]() ,点E是线段
,点E是线段![]() (不取端点A.B)上的一个动点,点F是射线
(不取端点A.B)上的一个动点,点F是射线![]() 上的一个动点,若
上的一个动点,若![]() 是四边形
是四边形![]() 的相似对角线,求
的相似对角线,求![]() 的长.(直接写出答案)
的长.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,2016年底全球支付宝用户数为4.5亿,2018年底达到9亿假设每年增长率相同,则按此速度增长,估计2019年底全球支付宝用户可达(![]() ≈1.414)( )
≈1.414)( )
A.11.25亿B.13.35亿C.12.73亿D.14亿
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:不相交的两个函数图象在竖直方向上的最短距离为这两个函数的“亲近距离”
(1)求抛物线y=x2﹣2x+3与x轴的“亲近距离”;
(2)在探究问题:求抛物线y=x2﹣2x+3与直线y=x﹣1的“亲近距离”的过程中,有人提出:过抛物线的顶点向x轴作垂线与直线相交,则该问题的“亲近距离”一定是抛物线顶点与交点之间的距离,你同意他的看法吗?请说明理由.
(3)若抛物线y=x2﹣2x+3与抛物线y=![]() +c的“亲近距离”为
+c的“亲近距离”为![]() ,求c的值.
,求c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
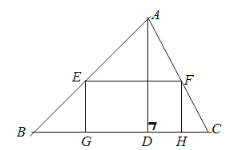
【题目】如图,AD是△ABC的高,点G、H在BC边上,点E在AB边上,点F在AC边上,BC=10cm,AD=8cm,四边形EFHG是矩形.
(1)△AEF与△ABC相似吗?请说明理由.
(2)若矩形EFHG的面积为15cm2,求这个矩形的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
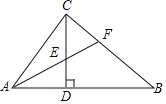
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB=50cm,拉杆BC的伸长距离最大时可达35cm,点A,B,C在同一条直线上,在箱体底端装有圆形的滚筒轮⊙A,⊙A与水平地面相切于点D,在拉杆伸长到最大的情况下,当点B距离水平地面34cm时,点C到水平地面的距离CE为55cm.设AF∥ MN.
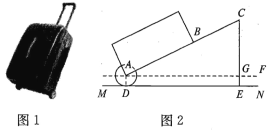
(1)求⊙A的半径.
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服,某人将手自然下垂在C端拉旅行箱时,CE为76cm,∠CAF=64°,求此时拉杆BC的伸长距离(结果精确到1cm,参考数据:sin64°≈0.9,cos64°≈0.39,tan64°≈2.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.
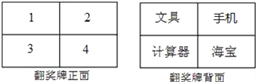
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
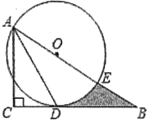
【题目】如图,已知在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D,以AB上点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=6,劣弧DE的长为π,求线段BD,BE与劣弧DE所围成的阴影部分的面积(结果保留根号和π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com