
【题目】已知:在四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF相交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF.求证:![]() ;
;
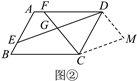
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=9,DA=DC=12,∠BAD=90°,DE⊥CF.求![]() 的值.
的值.

【答案】(1)详见解析;(2))当∠B=∠EGC或∠B+∠EGC=180°时,![]() 成立,证明详见解析;(3)
成立,证明详见解析;(3)![]() .
.
【解析】
(1)由矩形的性质得出∠A=∠ADC=90°,由角的互余关系整除∠ADE=∠DCF,即可得出△ADE∽△DCF;
(2)在AD的延长线上取点M,使CM=CF,由等腰三角形的性质得出∠CMF=∠CFM.由平行四边形的性质得出∠A=∠CDM,∠FCB=∠CFM,证出∠BEG+∠FCB=180°,得出∠AED=∠FCB,因此∠CMF=∠AED.证明△ADE∽△DCM,得出对应边成比例得![]() 即可得出结论;
即可得出结论;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出CM,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,建立方程求出求出CN,最后用相似三角形的性质即可得出结论.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∴∠ADE+∠CDG=90°.
∵DE⊥CF,
∴∠CDG+∠DCF=90°,
∴∠ADE=∠DCF.
又∵∠A=∠CGD=90°,
∴△ADE∽△GCD,
∴![]() 即
即![]()
(2)当∠B=∠EGC或∠B+∠EGC=180°时,![]() 成立.
成立.
证明:当∠B=∠EGC时,过点C作DE的平行线,过点D作CF的平行线,两线交于点M,如图①,∴四边形CMDG是平行四边形,
∴CG=DM,∠M=∠CGD,∠CDG=∠DCM.
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠A+∠B=180°,∠FCB=∠CFD.
∵∠B=∠EGC,∴∠A+∠EGC=180°.
∵∠EGC+∠CGD=180°,
∴∠A=∠CGD,
∴∠A=∠CGD=∠M.
∵AB∥CD,
∴∠AED=∠CDG.
∵∠CDG=∠DCM,
∴∠AED=∠DCM,
∴△ADE∽△MDC,
∴![]()
∵CG=DM,
∴![]()
即![]()
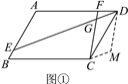
当∠B+∠EGC=180°时,过点C作DE的平行线,过点D作CF的平行线,两线交于点M,如图②,
∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠CFD=∠BCF.
∵∠B+∠EGC=180°,
∴∠GEB+∠BCF=180°,
∴∠BCF=∠AED,
∴∠CFD=∠AED.
∵∠ADE=∠GDF,
∴△FDG∽△EDA,
∴![]() ,即
,即![]()
∵AB∥CD,∴∠AED=∠CDE,
∴∠CFD=∠CDE.
∵∠FCD=∠DCG,
∴△FCD∽△DCG,
∴![]()
∴![]()
∴![]()
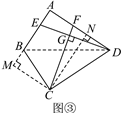
(3)如图③,过点C作CN⊥AD于点N,CM⊥AB交AB的延长线于点M,连接BD,设CN=x,
∵∠BAD=90°,
∴∠A=∠M=∠CAN=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM.
∵在△BAD和△BCD中,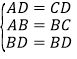
∴△BAD≌△BCD,
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°.
∵∠ABC+∠MBC=180°,
∴∠MBC=∠ADC.
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴![]() 即
即![]() ,∴
,∴![]()
在Rt△CMB中,![]() ,BM=AM-AB=x-9,
,BM=AM-AB=x-9,
由勾股定理,得BM2+CM2=BC2,
∴![]()
解得x1=0(舍去),![]()
∴![]()
∵∠A=∠FGE=90°,
∴∠AED+∠AFG=180°.
∵∠AFG+∠NFC=180°,
∴∠/span>AED=∠NFC.
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
![]()


科目:初中数学 来源: 题型:
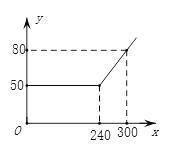
【题目】某网络公司推出了一系列上网包月业务,其中的一项业务是10M40元包240小时,且其中每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,小刚和小明家正好选择了这项上网业务.
(1)当x≥240时,求y与x之间的函数关系式;
(2)若小刚家10月份上网200小时,则他家应付多少元上网费?
(3)若小明家10月份上网费用为62元,则他家该月的上网时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,E,D是BC边的三等分点,F是AC的中点,BF分别交AD,AE于点G,H,则BG∶GH∶HF等于( )
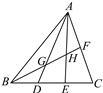
A. 1∶2∶3 B. 3∶5∶2 C. 5∶3∶2 D. 5∶3∶1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决(设DF=x,AD=y.)
保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求
保持(1)中条件不变,若DC=nDF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
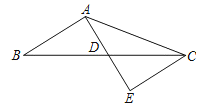
【题目】如图,在△ABC中,AB=3,AC=5,AD是BC边上的中线,且AD=2,延长AD到点E,使DE=AD,连接CE.
(1)求证:△AEC是直角三角形.
(2)求BC边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
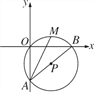
【题目】如图,在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上.
(1)求⊙P的半径及圆心P的坐标;
(2)M为劣弧OB的中点,求证:AM是∠OAB的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系xoy中,点A、B分别在x、y轴的正半轴上,将线段AB绕点B顺时针旋转90°,点A的对应点为点C.

(1)若A(6,0),B(0,4),求点C的坐标;
(2)以B为直角顶点,以AB和OB为直角边分别在第一、二象限作等腰Rt△ABD和等腰Rt△OBE,连DE交y轴于点M,当点A和点B分别在x、y轴的正半轴上运动时,判断并证明AO与MB的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com