
����Ŀ����֪������ֽƬABC�����С�C��90����AB��10��BC��6����E��F�ֱ���AC��AB�ϵĵ㣬����EF��
��1����ͼ1������ֽƬABC��EF�۵����۵����A�պ�����AB���ϵ�D������S��ADE=S�ı���BCED����ED�ij���
��2����ͼ2������ֽƬABC��EF�۵����۵����A�պ�����BC���ϵ�M������EM��AB��
�����ж��ı���AEMF����״����˵�����ɣ�
�����ۺ�EF�ij���
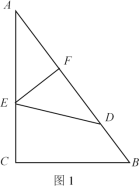
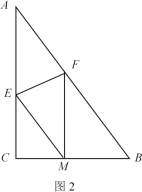
���𰸡���1��DE��5����2�����ı���AEMF�����Σ�֤������������![]()
��������
��1���������۵������ʵõ�EF��AB����AEF�ա�DEF����S��AEF��S��DEF������S��ABC��5S��AEF����֤��Rt��AEF��Rt��ABC��Ȼ��������������ε����ʵõ���������������Ⱥ�AB��AE�Ĺ�ϵ�������ù��ɶ������AB���ɵõ�AE�ij���
��2���������ı���ȵ��ı���������֤�����ɣ�
����AE��x����EM��x��CE��8x����֤����CME�ס�CBA�õ�����x�ı���ʽ�����x������CM��ֵ�������ù��ɶ��������AM��Ȼ��������ε������ʽ����EF��
��1���ߡ�ACB��һ����EF�۵����۵����A����AB���ϵĵ�D����
��EF��AB����AEF�ա�DEF��
��S��AEF��S��DEF��
��S��ADE��S�ı���BCDE��
��S��ABC��4S��AEF��
��Rt��ABC�У��ߡ�ACB��90![]() ��AB��10��BC��6��
��AB��10��BC��6��
��AC��8��
�ߡ�EAF����BAC��
��Rt��AEF��Rt��ABC��
��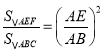 ����
����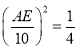 ��
��
��AE��5(��ֵ��ȥ)��
���۵�֪��DE��AE��5��
��2������ͼ2�У��ߡ�ACB��һ����EF�۵����۵����A����BC���ϵĵ�M����
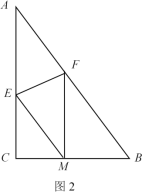
��AE��EM��AF��MF����AFE����MFE��
��ME��AB��
���AFE����FEM
���MFE����FEM��
��ME��MF��
��AE��EM��MF��AF��
���ı���AEMFΪ���Σ�
����AE��x����EM��x��CE��8x��
���ı���AEMFΪ���Σ�
��EM��AB��
���CME�ס�CBA��
��![]() ��
��
��![]() ��
��
���x��![]() ��CM��
��CM��![]() ��
��
��Rt��ACM��AM��![]() ��
��
��S����AEMF��![]() EFAM��AECM��
EFAM��AECM��
��EF��2��![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����AEF�У�AB=AE��BC=EF����B=��E��AB��EF��D���������н��ۣ���AF=AC����DF=CF���ۡ�AFC=��C���ܡ�BFD=��CAF��
������ȷ�Ľ��۸����У� ( )
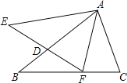
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
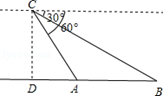
����Ŀ��ij�գ������ҹ��Ϻ�������ҵ��һ�Ҵ����洬ͻȻ�������飬��ز��Žӵ�����źź�������Dzһ��ֱ���ɻ���һ�Ҹ����Ϻ�Ѳ����������ǰ����Ԯ�����ɻ�������뺣��3000�ĸ߿�C�������A���������ĸ���Ϊ60�������B�����������洬�ĸ���Ϊ30�������ʣ���ʱ���������洬����Զ��������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
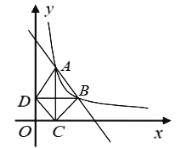
����Ŀ����ͼ����ֱ������ƽ���ڣ�����![]() ��x��0��m�dz�������ͼ��A(1��4)��B(a��b)������a��1������A��x�ᴹ�ߣ�����ΪC������B��y�ᴹ�ߣ�����ΪD������AD��DC��CB
��x��0��m�dz�������ͼ��A(1��4)��B(a��b)������a��1������A��x�ᴹ�ߣ�����ΪC������B��y�ᴹ�ߣ�����ΪD������AD��DC��CB
��1������ABD�����Ϊ4�����B��������
��2����֤��DC��AB.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�濿ǽ(ǽ�������ó���Ϊ8 m)�Ŀյ����ó�Ϊ24 m�����Χ���м���ж�����ʵij����λ��ԣ��軨�ԵĿ�ABΪx m�����ΪS m2.
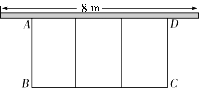
��1����S����x�ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
��2������Χ�ɻ��Ե�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����DEF�У���������AB=DE������Ҫ����������������ʹ��ABC�ա�DEF���������ӵ�һ�������ǣ� ��
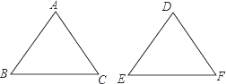
A. ��B=��E��BC=EF B. ��A=��D��BC=EF
C. ��A=��D����B=��E D. BC=EF��AC=DF
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
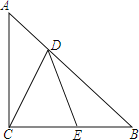
����Ŀ����ͼ��![]() �У�
��![]() ����
����![]() ��
��![]() �ϣ�
�ϣ�![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��
![]() ��֤
��֤![]() ��
��
![]() ��
��![]() �Ķ�����
�Ķ�����
![]() ��
��![]() ��
��![]() ��
��![]() �������
�������![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y1=��x+4��y2=![]() x+b����˫����y=
x+b����˫����y=![]() ���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
���ڵ�A��1��m����������ֱ�߷ֱ���x�ύ��B��C���㣮
��1����y��x֮��ĺ�����ϵʽ��
��2��ֱ��д����x��0ʱ������ʽ![]() x+b��
x+b��![]() �Ľ⼯��
�Ľ⼯��
��3������P��x���ϣ�����AP����ABC������ֳ�1��3�����֣����ʱ��P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
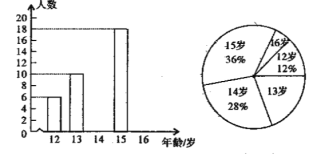
����Ŀ��ij��ѧ��ѧ��ȤС��Ϊ���˽ⱾУѧ���������������������˸�У����ѧ�������䣬�������ݲ��������²�������ͳ��ͼ������������Ϣ������⣺
��1���˴ι������˶����ˣ�
��2��������![]() �ꡱ������ͳ��ͼ����ռԲ�ĽǵĶ�����
�ꡱ������ͳ��ͼ����ռԲ�ĽǵĶ�����
��3���뽫����ͳ��ͼ����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com