
【题目】已知:等边△ABC中,E在BC的延长线上,CF平分∠ACE,P为射线BC上一点,Q为CF上一点,连接AP、PQ.
(Ⅰ)若BP=QC,求证:AP=PQ;
(Ⅱ)若AP=PQ,求∠APQ的度数.


【答案】(1)见解析;(2)60°.
【解析】
(1)连接AQ,根据等边三角形的性质,得出AB=AC=BC,∠B=∠BAC=∠ACB=∠ACF= 60°,根据SAS求得△ABP≌△ACQ,得出AP=AQ,∠BAP=∠CAQ,可得出∠PAQ= 60°,则△PAQ是等边三角形,即可求得AP=PQ;
(2)在CF上截取CQ′=BP,根据等边三角形的性质,得出AB=AC=BC,∠B=∠ACB=60°,根据SAS求得△ABP≌△ACQ′,得出△PAQ′是等边三角形,从而证得Q′和Q是同一点,即可求得∠APQ=60°.
证明:(1)连接AQ,
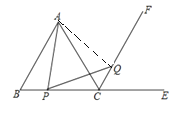
∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠BAC=∠ACB = 60°,
∴∠ACE=120°,
∵CF平分∠ACE,
∴∠ACQ=60°=∠B,
在△ABP与△ACQ中,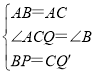
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ,
∴∠CAQ+∠PAC=∠BAP+∠PAC=60°
即∠PAQ=60°,
∴△PAQ是等边三角形,
∴AP=PQ;
(2)解:在CF上截取CQ′=BP,
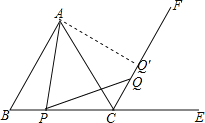
∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠ACB=60°,
∴∠ACE=120°,
∵CF平分∠ACE,
∴∠ACQ=60°=∠B,
在△ABP与△ACQ′中,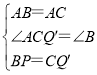
∴△ABP≌△ACQ′(SAS),
∴AP=AQ′,∠BAP=∠CAQ′,
∴∠CAQ′+∠PAC=∠BAP+∠PAC=60°
即∠PAQ′=60°,
∴△PAQ′是等边三角形,
∴AP=PQ′,∠APQ′=60°
∵AP=PQ,
∴PQ=PQ′,
∴Q′和Q是同一点,
∴∠APQ=60°.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点D为AB下方⊙O上一点,点C为弧ABD的中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CH⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长度.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是经过∠BCA顶点C的一条直线,且直线CD经过∠BCA的内部,点E,F在射线CD上,已知CA=CB且∠BEC=∠CFA=∠α.

(1)如图1,若∠BCA=80°,∠α=90°,问EF=BE-AF,成立吗?说明理由.
(2)将(1)中的已知条件改成∠BCA=∠β,∠α+∠β=180°(如图2),问EF=BE-AF仍成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x与反比例函数y=![]() (x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B.
(x>0)的图象交于点A(4,n),AB⊥x轴,垂足为B.
(1)求k的值;
(2)点C在AB上,若OC=AC,求AC的长;
(3)点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
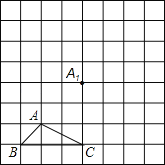
【题目】如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
(1)把△ABC沿BA方向平移后,点A移到点A1,在网格中画出平移后得到的△A1B1C1;
(2)把△A1B1C1绕点A1按逆时针方向旋转90°,在网格中画出旋转后的△A1B2C2;
(3)如果网格中小正方形的边长为1,求点B经过(1)、(2)变换的路径总长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com