
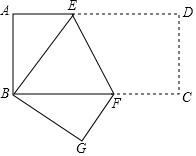
 如图,矩形ABCD中,AB=6,CB=18,若将矩形折叠使B与D重合,则折痕EF的长为2$\sqrt{10}$.
如图,矩形ABCD中,AB=6,CB=18,若将矩形折叠使B与D重合,则折痕EF的长为2$\sqrt{10}$. 分析 首先由折叠的性质知BE=ED,∠BEH=∠DEH,可得△BDE是等腰三角形,再根据等腰三角形的性质可得BH=HD,BD⊥EF,再在Rt△ABD中,利用勾股定理算出BD的长,再在Rt△ABE中利用勾股定理计算出AE的长,进而得到ED的长,再次利用勾股定理计算出EH的长,然后证明△BHF≌△DHE,继而得到HF=EH,从而得到EF的长.
解答 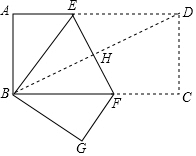 解:连接BD,交EF于点H,
解:连接BD,交EF于点H,
由折叠的性质知,BE=ED,∠BEH=∠DEH,
则△BDE是等腰三角形,
∵∠BEH=∠DEH,
∴BH=HD,BD⊥EF(顶角的平分线是底边上的高,是底边上的中线),
在Rt△ABD中,BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{36+324}$=6$\sqrt{10}$,
∵BH=DH,
∴DH=$\frac{1}{2}$DB=3$\sqrt{10}$,
设AE=x,则DE=BE=18-x,
在Rt△ABE中:AE2+AB2=BE2,
则x2+62=(18-x)2,
解得:x=8,
则ED=18-8=10,
在Rt△EDH中:EH2+DH2=ED2,
EH=$\sqrt{E{D}^{2}-D{H}^{2}}$=$\sqrt{10}$,
∵BD⊥EF,
∴∠BHF=∠EHD=90°,
∵AD∥CB,
∴∠EDH=∠HBF,
在△BHF与△DHE中,
$\left\{\begin{array}{l}{∠BHF=∠EHD}\\{BH=DH}\\{∠EDH=∠HBF}\end{array}\right.$,
∴△BHF≌△DHE,
∴HF=EH=$\sqrt{10}$,
∴EF=2$\sqrt{10}$.
故答案为:2$\sqrt{10}$.
点评 此题主要考查了折叠的性质,以及勾股定理的应用,关键是熟练掌握勾股定理:直角三角形中,两直角边的平方和等于斜边的平方.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
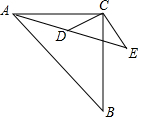 如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.
如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AE上,若AC=10,AD=2$\sqrt{10}$,求DC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
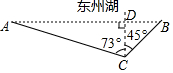 某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.
某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题:
某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:20170-(-$\frac{1}{3}$)-1
(1)计算:20170-(-$\frac{1}{3}$)-1查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com