
【题目】如图,在平面直角坐标系中,抛物线与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(﹣3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.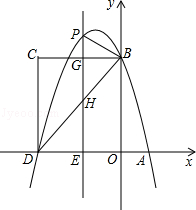
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
【答案】
(1)
解:设抛物线解析式为y=a(x﹣1)(x+3),
把B(0,4)代入得a(﹣1)3=4,解得a=﹣ ![]() ,
,
所以抛物线解析式为y=﹣ ![]() (x﹣1)(x+3),
(x﹣1)(x+3),
即y=﹣ ![]() x2﹣
x2﹣ ![]() x+4
x+4
(2)
解:当y=4时,﹣ ![]() x2﹣
x2﹣ ![]() x+4=4,解得x1=0,x2=﹣2,
x+4=4,解得x1=0,x2=﹣2,
∴﹣2<m<0,
∵E(m,0),PE⊥x轴,
∴P(m,﹣ ![]() m2﹣
m2﹣ ![]() m+4),
m+4),
而BC∥x轴,
∴G(m,4),
∴PG=﹣ ![]() m2﹣
m2﹣ ![]() m+4﹣4=﹣
m+4﹣4=﹣ ![]() m2﹣
m2﹣ ![]() m(﹣2<m<0)
m(﹣2<m<0)
(3)
解:∵HE∥OB,
∴△DEH∽△DOB,
∵∠PGB=∠DOB,
∴当 ![]() =
= ![]() 时,△PGB∽△BOD,则△PGB∽△HED,
时,△PGB∽△BOD,则△PGB∽△HED,
即 ![]() =
= ![]() ,整理得m2+m=0,解得m1=0(舍去),m2=﹣1,
,整理得m2+m=0,解得m1=0(舍去),m2=﹣1,
当 ![]() =
= ![]() 时,△PGB∽△DOB,则△PGB∽△DEH,
时,△PGB∽△DOB,则△PGB∽△DEH,
即 ![]() =
= ![]() ,整理得16m2+23m=0,解得m1=0(舍去),m2=﹣
,整理得16m2+23m=0,解得m1=0(舍去),m2=﹣ ![]() ,
,
综上所述,在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为﹣1或﹣ ![]()
【解析】(1)设交点式y=a(x﹣1)(x+3),然后把B点坐标代入求出a即可得到抛物线解析式;(2)先解方程﹣ ![]() x2﹣
x2﹣ x+4=4,解得x1=0,x2=﹣2,则﹣2<m<0,设P(m,﹣
![]() m2﹣
m2﹣ ![]() m+4),G(m,4),则可用m表示PG;(3)易得△DEH∽△DOB,则判定△PGB与△BOD,由于∠PGB=∠DOB,根据相似三角形的判定方法,当
m+4),G(m,4),则可用m表示PG;(3)易得△DEH∽△DOB,则判定△PGB与△BOD,由于∠PGB=∠DOB,根据相似三角形的判定方法,当 ![]() =
= ![]() 时,△PGB∽△BOD,则△PGB∽△HED,当
时,△PGB∽△BOD,则△PGB∽△HED,当 ![]() =
= ![]() 时,△PGB∽△DOB,则△PGB∽△DEH,然后分别利用相似比列关于m的方程,再解方程求出m,从而得到满足条件的m的值.
时,△PGB∽△DOB,则△PGB∽△DEH,然后分别利用相似比列关于m的方程,再解方程求出m,从而得到满足条件的m的值.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为度. 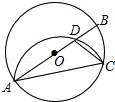
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为筹备校庆活动,准备印制一批校庆纪念册,该纪念册每册需要10张8K大小的纸,其中4张为彩色页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩色页300元/张,黑白页50元/张;印刷费与印数的关系见表.
印数a (单位:千册) | 1≤a<5 | 5≤a<10 |
彩色 (单位:元/张) | 2.2 | 2.0 |
黑白(单位:元/张) | 0.7 | 0.6 |
(1)直接写出印制这批纪念册的制版费为多少元;
(2)若印制6千册,那么共需多少费用?
(3)如印制x(1≤x<10)千册,所需费用为y元,请写出y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2i=﹣i,i4=(i2)2=(﹣1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4ni=i,同理可得i4n+2=﹣1,i4n+3=﹣i,i4n=1.
计算:(1)i.i2.i3.i4
(2)i+i2+i3+i4+…+i2017+i2018.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给下面命题的说理过程填写依据.
已知:如图,直线AB,CD相交于点O,EO⊥CD,垂足为O,OF平分∠BOD,对∠EOF=![]() ∠BOC说明理由.
∠BOC说明理由.
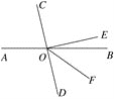
理由:因为∠AOC=∠BOD( ),
∠BOF=![]() ∠BOD( ),
∠BOD( ),
所以∠BOF=![]() ∠AOC( ).
∠AOC( ).
因为∠AOC=180°-∠BOC( ),
所以∠BOF=90°-![]() ∠BOC.
∠BOC.
因为EO⊥CD( ),
所以∠COE=90°( )
因为∠BOE+∠COE=∠BOC( ),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°( )
因为∠EOF=∠BOE+∠BOF( )
所以∠EOF=(∠BOC-90°)+(90°![]() ∠BOC)( )
∠BOC)( )
所以∠EOF=![]() ∠BOC.
∠BOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=2x-4
(1)画出函数的图象;
(2)判断点A(1,-2),B(2,1)是否在该函数的图象上.
(3)已知点A(-2,b)在该函数图像上,求b值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+3的图象与反比例y= ![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com