
【题目】二次函数 ![]() 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题:
(1)写出不等式 ![]() 的解集;
的解集;
(2)写出 ![]() 随
随 ![]() 的增大而减小的自变量
的增大而减小的自变量 ![]() 的取值范围;
的取值范围;
(3)分别求出 ![]() 的值.
的值.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
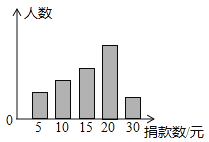
【题目】松雷中学校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,下图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8:2,又知此次调查中捐15元和20元的人数共39人.
(1)他们一共抽查了多少人?
(2)若该校共有2310名学生,请估计全校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程.
(1)(x﹣3)2=2(x﹣3);
(2)9x2﹣3=22;
(3)x2﹣6x﹣98=0;
(4)3x2﹣1=2x+2;
(5)(3m+2)2﹣7(3m+2)+10=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点B的坐标为(6,4).
(1)请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线AC是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.
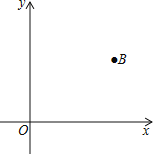
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户种植花生,原来种植的花生亩产量为200千克,出油率为50%(即每100千克花生可加工成花生油50千克).现在种植新品种花生后,每亩收获的花生可加工成花生油132千克,其中花生出油率的增长率是亩产量的增长率的二分之一.则新品种花生亩产量的增长率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
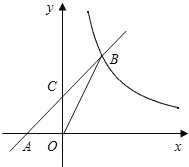
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点; ②4a+b+c=0; ③a+b>0; ④该二次函数的最小值为b;⑤当0<x<4时,y>0.正确的是( )
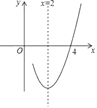
A. ①② B. ③④⑤ C. ①②④ D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
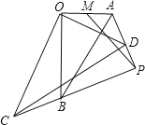
【题目】如图,Rt△AOB∽△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=6,OB=8,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最小值____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com