
【题目】如图,点E是正方形ABCD内的一点,点![]() 在BC边的下方,连接AE,BE,CE,
在BC边的下方,连接AE,BE,CE,![]() ,
,![]() 若
若![]() ,
,![]() ,
,![]() ,且
,且![]() ≌
≌![]() ,则
,则![]() ______
______ ![]()
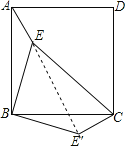
【答案】135
【解析】
先由全等三角形的性质证明△EBE′是等腰直角直角三角形,进而得出∠BEE′=∠BE′E=45°,由勾股定理求出EE′2的值,再勾股定理的逆定理证得△EE′C是直角三角形,从而∠EE′C=90°,即可得出答案.
连接EE′.
∵△ABE≌△CBE′,
∴∠ABE=∠CBE′,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠EBE′=90°,
∴△EBE′是直角三角形,
又∵△ABE≌△CBE′,
∴BE=BE′=2,∠AEB=∠BE′C,
∴∠BEE′=∠BE′E=45°,
∵EE′2=22+22=8,AE=CE′=1,EC=3,
∴EC2=E′C2+EE′2,
∴△EE′C是直角三角形,
∴∠EE′C=90°,
∴∠AEB=135°,
故答案为:135.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):

①接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
②若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
③若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
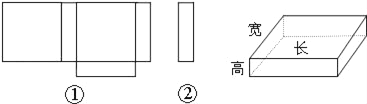
(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
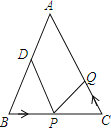
【题目】![]() 中,
中,![]() 厘米,
厘米,![]() ,
,![]() 厘米,点D为AB的中点
厘米,点D为AB的中点![]() 如果点P在线段BC上以v厘米
如果点P在线段BC上以v厘米![]() 秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动
秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动![]() 若点Q的运动速度为3厘米
若点Q的运动速度为3厘米![]() 秒,则当
秒,则当![]() 与
与![]() 全等时,v的值为
全等时,v的值为![]()
![]()
A. ![]() B. 3 C.
B. 3 C. ![]() 或3 D. 1或5
或3 D. 1或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第( )秒
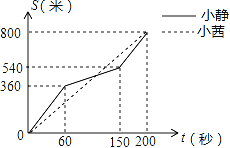
A. 80 B. 105 C. 120 D. 150
查看答案和解析>>
科目:初中数学 来源: 题型:
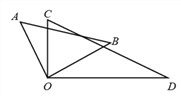
【题目】如图,将一副三角尺的直角顶点重合在一起.
(1)若 OB 是∠DOC 的角平分线,求∠AOD 的补角的度数是多少?
(2)若 ∠COB 与 ∠DOA 的比是 2:7,求 ∠BOC 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y= ![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )
A.25 ![]()
B.18 ![]()
C.9 ![]()
D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com