
【题目】已知:点 A(4,0),点 B 是 y 轴正半轴上一点,如图 1,以 AB 为直角边作等腰直角三角形 ABC ABC 90.
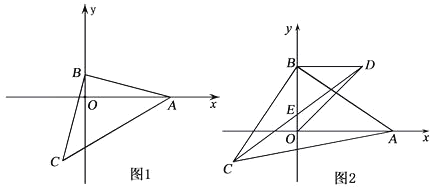
(1)若 AC 6,求点B 的坐标;
(2)当点B 坐标为(0,1)时,求点C 的坐标;
(3)如图 2,以 OB 为直角边作等腰直角△OBD,点D在第一象限,连接CD交 y 轴于点E.在点 B 运动的过程中,BE 的长是否发生变化?若不变,求出 BE 的长;若变化,请说明理由.
【答案】(1)(0,![]() ) (2)(-1,-3) (3)BE长保持不变,BE的长为2
) (2)(-1,-3) (3)BE长保持不变,BE的长为2
【解析】
(1)根据AC的长求出AB的长,再用勾股定理求B点坐标.
(2)过C作CM⊥y轴于M,通过判定△BCM≌△ABO(AAS),得出CM=BO=1,BM=AO=4,进而得到OM=3,据此可得C(-1,-3);
(3)过C作CM⊥y轴于M,根据△BCM≌△ABO,可得CM=BO,BM=OA=4,再判定△DBE≌△CME(AAS),可得BE=EM,进而得到BE=![]() BM=2.
BM=2.
(1)∵△ABC是等腰直角三角形,AC 6
∴2AB2=36
∴AB=![]()
设B点坐标为(0,a)(a>0)
在直角三角形AOB中,A(4,0)
∴16+a2=18
∴a=![]()
∴B点的坐标为(0,![]() )
)
(2)如图1,过C作CM⊥y轴于M.
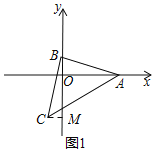
∵CM⊥y轴,
∴∠BMC=∠AOB=90°,
∴∠ABO+∠BAO=90°
∵∠ABC=90°,
∴∠CBM+∠ABO=90°,
∴∠CBM=∠BAO,
在△BCM与△ABO中,
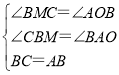 ,
,
∴△BCM≌△ABO(AAS),
∴CM=BO=1,BM=AO=4,
∴OM=3,
∴C(-1,-3);
(3)在B点运动过程中,BE长保持不变,BE的长为2,
理由:如图2,过C作CM⊥y轴于M,
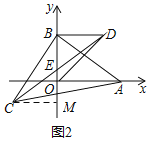
由(1)可知:△BCM≌△ABO,
∴CM=BO,BM=OA=4.
∵△BDO是等腰直角三角形,
∴BO=BD,∠DBO=90°,
∴CM=BD,∠DBE=∠CME=90°,
在△DBE与△CME中,
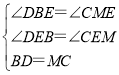 ,
,
∴△DBE≌△CME(AAS),
∴BE=EM,
∴BE=![]() BM=2.
BM=2.


科目:初中数学 来源: 题型:
【题目】以直线AB上一点O为端点作射线OC,将一块直角三角板的直角顶点放在O处(注:∠DOE=90°).



(1)如图①,若直角三角板DOE的一边OD放在射线OB上,且∠BOC=60°,求∠COE的度数;
(2)如图②,将三板DOE绕O逆时针转动到某个位置时,若恰好满足5∠COD=∠AOE,且∠BOC=60°,求∠BOD的度数;
(3)如图③,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OE恰好平分∠AOC,请说明OD所在射线是∠BOC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校招生时,2640名学生的成绩数据分别由两位程序操作员各向计算机输入一遍,已知甲的输入速度是乙的2倍,结果甲比乙少用2小时输完.问这两个操作员每分钟各能输入多少名学生的成绩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,与BC相交于点F,过点B作BE⊥AD于点D,交AC延长线于点E,过点C作CH⊥AB于点H,交AF于点G,则下列结论:![]() ⑤
⑤![]() ;正确的有( )个.
;正确的有( )个.
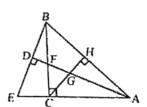
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
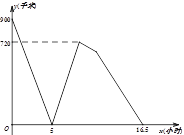
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达
两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达![]() 地后马上以另一速度原路返回
地后马上以另一速度原路返回![]() 地(掉头的时间忽略不计),乙车到达
地(掉头的时间忽略不计),乙车到达![]() 地以后即停在
地以后即停在![]() 地等待甲车.如图所示为甲乙两车间的距离
地等待甲车.如图所示为甲乙两车间的距离![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (小时)之间的函数图象,则当乙车到达
(小时)之间的函数图象,则当乙车到达![]() 地的时候,甲车与
地的时候,甲车与![]() 地的距离为__________千米.
地的距离为__________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小苏和小林在如图所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如下图所示.下列叙述正确的是( )


A. 两人从起跑线同时出发,同时到达终点
B. 小苏跑全程的平均速度大于小林跑全程的平均速度
C. 小苏前15s跑过的路程大于小林前15s跑过的路程
D. 小林在跑最后100m的过程中,与小苏相遇2次
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com