
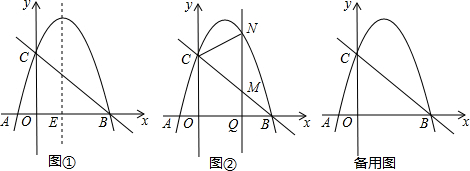
���� ��1�����ݶԳ��ṫʽ���������E���꣬��y=0���ⷽ�̼��������A���꣮
��2����ͼ���У����E��ֱ��BC�����ڵ�D������DE����DE��BC����tan��OBC=$\frac{DE}{BD}$=$\frac{OC}{OB}$���г����̼��ɽ����
��3�����������ٵ�N��ֱ��BC�Ϸ����ڵ�N��ֱ��BC�·����ֱ��г����̼��ɽ����
��� �⣺��1���߶Գ���x=-$\frac{-3a}{2a}$=$\frac{3}{2}$��
���E���꣨$\frac{3}{2}$��0����
��y=0������ax2-3ax-4a=0��
��x=-1��4��
���A���꣨-1��0����
�ʴ𰸷ֱ�Ϊ��$\frac{3}{2}$��0������-1��0����
��2����ͼ���У����E��ֱ��BC�����ڵ�D������DE����DE��BC��
��DE=OE=$\frac{3}{2}$��EB=$\frac{5}{2}$��OC=-4a��
��DB=$\sqrt{E{B}^{2}-D{E}^{2}}$=$\sqrt{2��{5}^{2}-1��{5}^{2}}$=2��
��tan��OBC=$\frac{DE}{BD}$=$\frac{OC}{OB}$��
��$\frac{1.5}{2}$=$\frac{-4a}{3}$��
��a=-$\frac{3}{4}$��
�������߽���ʽΪy=-$\frac{3}{4}$x2+$\frac{9}{4}$x+3��
��3����ͼ���У��������M��CN=��NCB��
��MN��OM�䣬
���M��CN=��CNM��
��MN=CM��
��ֱ��BC����ʽΪy=-$\frac{3}{4}$x+3��
��M��m��-$\frac{3}{4}$m+3����N��m��-$\frac{3}{4}$m2+$\frac{9}{4}$m+3������MF��OC��F��
��sin��BCO=$\frac{FM}{MC}$=$\frac{BO}{BC}$��
��$\frac{m}{CM}$=$\frac{4}{5}$��
��CM=$\frac{5}{4}$m��
�ٵ�N��ֱ��BC�Ϸ�ʱ��-$\frac{3}{4}$x2+$\frac{9}{4}$x+3-��-$\frac{3}{4}$x+3��=$\frac{5}{4}$m��
��ã�m=$\frac{7}{3}$��0����������
��Q1��$\frac{7}{3}$��0����
�ڵ�N��ֱ��BC�·�ʱ����-$\frac{3}{4}$m+3��-��-$\frac{3}{4}$m2+$\frac{9}{4}$m+3��=$\frac{5}{4}$m��
���m=$\frac{17}{3}$��0����������
��Q2��$\frac{17}{3}$��0����
������������Q������$\frac{7}{3}$��0����$\frac{17}{3}$��0����
���� ���⿼����κ����ۺ��⡢Բ�����۱任�����Ǻ�����һ�κ�����֪ʶ������Ĺؼ���ͨ�����Ǻ����������̣�������ת��Ϊ���̽���������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
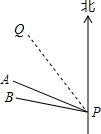 ��ͼ��̨������λ�ڵ�P�������ر�ƫ��30�㷽��PQ�ƶ�����̨֪�������ƶ����ٶ���30km/h����̨��Ӱ������İ뾶Ϊ200km��A��λ�ڵ�P�ı�ƫ��60�㷽���ϣ����P�ľ���Ϊ200$\sqrt{3}$km����B��λ�ڵ�P�ı�ƫ��75�㷽���ϣ����P�ľ���Ϊ210$\sqrt{2}$km����
��ͼ��̨������λ�ڵ�P�������ر�ƫ��30�㷽��PQ�ƶ�����̨֪�������ƶ����ٶ���30km/h����̨��Ӱ������İ뾶Ϊ200km��A��λ�ڵ�P�ı�ƫ��60�㷽���ϣ����P�ľ���Ϊ200$\sqrt{3}$km����B��λ�ڵ�P�ı�ƫ��75�㷽���ϣ����P�ľ���Ϊ210$\sqrt{2}$km�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABCD��A��1��2��������ABCD�����Ϊ8��˫����y=$\frac{k}{x}$���þ�����B��D�����㣬��AB��x�ᣬ��k��ֵ��
��ͼ����ABCD��A��1��2��������ABCD�����Ϊ8��˫����y=$\frac{k}{x}$���þ�����B��D�����㣬��AB��x�ᣬ��k��ֵ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com