
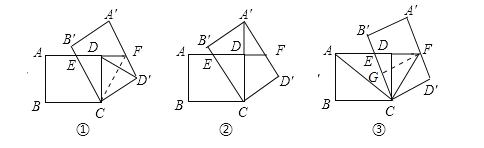
【题目】如图,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',B'C与AD交于点E,AD的延长线与A'D'交于点F.

(1)如图①,当α=60°时,连接DD',求DD'和A'F的长;
(2)如图②,当矩形A'B'CD'的顶点A'落在CD的延长线上时,求EF的长;
(3)如图③,当AE=EF时,连接AC,CF,求ACCF的值.
【答案】(1)DD′=3,A′F= 4﹣![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)①如图①中,∵矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',只要证明△CDD′是等边三角形即可解决问题;
②如图①中,连接CF,在Rt△CD′F中,求出FD′即可解决问题;
(2)由△A′DF∽△A′D′C,可推出DF的长,同理可得△CDE∽△CB′A′,可求出DE的长,即可解决问题;
(3)如图③中,作FG⊥CB′于G,由S△ACF=![]() ACCF=
ACCF=![]() AFCD,把问题转化为求AFCD,只要证明∠ACF=90°,证明△CAD∽△FAC,即可解决问题;
AFCD,把问题转化为求AFCD,只要证明∠ACF=90°,证明△CAD∽△FAC,即可解决问题;
试题解析:(1)①如图①中,∵矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',∴A′D′=AD=B′C=BC=4,CD′=CD=A′B′=AB=3∠A′D′C=∠ADC=90°,∵α=60°,∴∠DCD′=60°,∴△CDD′是等边三角形,∴DD′=CD=3.
②如图①中,连接CF.∵CD=CD′,CF=CF,∠CDF=∠CD′F=90°,∴△CDF≌△CD′F,∴∠DCF=∠D′CF=![]() ∠DCD′=30°,在Rt△CD′F中,∵tan∠D′CF=
∠DCD′=30°,在Rt△CD′F中,∵tan∠D′CF=![]() ,∴D′F=
,∴D′F=![]() ,∴A′F=A′D′﹣D′F=4﹣
,∴A′F=A′D′﹣D′F=4﹣![]() .
.
(2)如图②中,在Rt△A′CD′中,∵∠D′=90°,∴A′C2=A′D′2+CD′2,∴A′C=5,A′D=2,∵∠DA′F=∠CA′D′,∠A′DF=∠D′=90°,∴△A′DF∽△A′D′C,∴![]() ,∴
,∴![]() ,∴DF=
,∴DF=![]() ,同理可得△CDE∽△CB′A′,∴
,同理可得△CDE∽△CB′A′,∴![]() ,∴
,∴![]() ,∴ED=
,∴ED=![]() ,∴EF=ED+DF=
,∴EF=ED+DF=![]() .
.
(3)如图③中,作FG⊥CB′于G.,∵四边形A′B′CD′是矩形,∴GF=CD′=CD=3,∵S△CEF=![]() EFDC=
EFDC=![]() CEFG,∴CE=EF,∵AE=EF,∴AE=EF=CE,∴∠ACF=90°,∵∠ADC=∠ACF,∠CAD=∠FAC,∴△CAD∽△FAC,∴
CEFG,∴CE=EF,∵AE=EF,∴AE=EF=CE,∴∠ACF=90°,∵∠ADC=∠ACF,∠CAD=∠FAC,∴△CAD∽△FAC,∴![]() ,∴AC2=ADAF,∴AF=
,∴AC2=ADAF,∴AF=![]() ,∵S△ACF=
,∵S△ACF=![]() ACCF=
ACCF=![]() AFCD,∴ACCF=AFCD=
AFCD,∴ACCF=AFCD=![]() .
.


科目:初中数学 来源: 题型:
【题目】长城总长约6700010米,用科学计数法表示是( )(保留两个有效数字)
A.67×105米B.6.7×106米C.6.7×105米D.0.67×107米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D在AB上,点E与点C在AB的两侧,连接BE,CD,点M、N分别是BE、CD的中点,连接MN,AM,AN.
下列结论:①△ACD≌△ABE;②△ABC∽△AMN;③△AMN是等边三角形;④若点D是AB的中点,则S△ABC=2S△ABE.
其中正确的结论是 .(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两条直线被第三条直线所截,下列四个说法中正确的个数是( )
(1)同位角的角平分线互相平行;(2)内错角的角平分线互相平行;(3)同旁内角的角平分线互相垂直;(4)邻补角的角平分线互相垂直
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,设
中,设![]() 的对边分别为
的对边分别为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,会有
,会有![]() ,则
,则

![]() ,即
,即![]()
同理![]() ,
,![]()
通过推理还可以得到另一个表达三角形边角关系的定理—余弦定理:

在![]() 中,若
中,若![]() 的对边分别为
的对边分别为![]() ,则
,则
![]()
![]()
![]()
用上面的三角形面积公式和余弦定理解决问题:
(1)如图,在![]() 中,
中,![]() ,
,![]() 的对边分别是3和8.
的对边分别是3和8.

求![]() 和
和![]() .
.
解:![]() _______________;
_______________;
![]() ______________.
______________.
(2)在![]() 中,已知
中,已知![]() ,
,![]() 分别是以
分别是以![]() 为边长的等边三角形,设
为边长的等边三角形,设![]() 的面积分别为
的面积分别为![]() ,求证:
,求证: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于条件:①两条直角边对应相等;②斜边和一锐角对应相等;③斜边和一直角边对应相等;④一直角边和一锐角对应相等;以上能判定两直角三角形全等的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com