
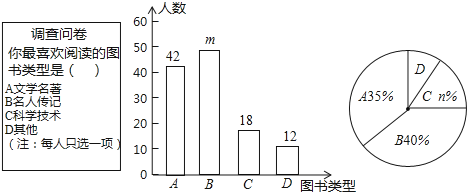
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
【答案】(1)120,48,15;(2)336;(3)![]() .
.
【解析】试题分析:(1)用A类的人数除以所占的百分比求出总人数,用总数减去A,C,D类的人数,即可求出m的值,用C类的人数除以总人数,即可得出n的值;
(2)用该校喜欢阅读“A”类图书的学生人数=学校总人数×A类的百分比求解即可;
(3)列出图形,即可得出答案.
试题解析:(1)这次调查的学生人数为42÷35%=120(人),m=120﹣42﹣18﹣12=48,18÷120=15%;所以n=15,故答案为:120,48,15;
(2)该校喜欢阅读“A”类图书的学生人数为:960×35%=336(人);
(3)抽出的所有情况如图:
![]()
两名参赛同学为1男1女的概率为: ![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边AB,BC上,∠ADE=∠CDF.
(1)求证:AE=CF;
(2)连接DB交EF于点O,延长OB至G,使OG=OD,连接EG,FG,判断四边形DEGF是否是菱形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.

(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全图形,并直接写出EF、EQ、BP三者之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解2018年度下学期七年级数学学科期末考试各分数段成绩的分布情况,从全校七年级1200名学生中随机抽取了200名学生的期末数学成绩进行调查,在这次调查中,样本是( )
A. 1200名学生 B. 200名学生
C. 1200名学生的期末数学成绩 D. 200名学生的期末数学成绩
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的一点P,且抛物线L的顶点Q在直线l上,则称此直线l与该抛物线L具有“一带一路”关系.此时,直线l叫做抛物线L的“带线”,抛物线L叫做直线l的“路线”.
(1)若直线y=mx+1与抛物线y=x2﹣2x+n具有“一带一路”关系,求m,n的值;
(2)若某“路线”L的顶点在反比例函数y=![]() 的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
的图象上,它的“带线”l的解析式为y=2x﹣4,求此“路线”L的解析式;
(3)当常数k满足![]() ≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
≤k≤2时,求抛物线L:y=ax2+(3k2﹣2k+1)x+k的“带线”l与x轴,y轴所围成的三角形面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com