
 正方形ABCD中,点EF分别在边BC和CD上,且AE⊥BF.点C关于自线BF的对称点为点G,连线FG并延长交AD于点H,若点H是AD的三等分点,则的$\frac{BE}{BC}$值为$\frac{1}{5}$或$\frac{11}{12}$.
正方形ABCD中,点EF分别在边BC和CD上,且AE⊥BF.点C关于自线BF的对称点为点G,连线FG并延长交AD于点H,若点H是AD的三等分点,则的$\frac{BE}{BC}$值为$\frac{1}{5}$或$\frac{11}{12}$. 分析 如图,连接BG、BH.首先证明△BHA≌△BHG,△ABE≌△BCF,推出AH=GH,CF=BE,分两种情形讨论①当AH=2a,DH=a时,设CF=b,②当AH=a,DH=2a时,设CF=b,
利用勾股定理列出方程求出a、b关系即可解决问题.
解答 解:如图,连接BG、BH.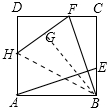
∵C、G关于BF对称,
∴CF=FG,BC=BG=AB,∠C=∠BGF=90°,
在Rt△BHA和Rt△BHG中,
$\left\{\begin{array}{l}{BH=BH}\\{BA=BG}\end{array}\right.$,
∴△BHA≌△BHG.
∴AH=GH,
∵AE⊥BF,
∴∠BAE+∠AEB=90°,∠AEB+∠CBF=90°,
∴∠BAE=∠FBC,∵AB=BC,∠ABE=∠C,
∴△ABE≌△BCF,
∴CF=BE,
设AB=BC=CD=AD=3a,
①当AH=2a,DH=a时,设CF=b,
在Rt△DHF中,∵DH2+DF2=HF2,
∴a2+(3a-b)2=(2a+b)2,
∴b=$\frac{3}{5}$a,
∴$\frac{BE}{BC}$=$\frac{\frac{3}{5}a}{3a}$=$\frac{1}{5}$,
②当AH=a,DH=2a时,设CF=b,同理可得,(2a)2+(3a-b)2=(a+b)2,
∴b=$\frac{11}{4}a$,
∴$\frac{BE}{BC}$=$\frac{\frac{11}{4}a}{3a}$=$\frac{11}{12}$,
综上所述$\frac{BE}{BC}$=$\frac{1}{5}$或$\frac{11}{12}$.
故答案为$\frac{1}{5}$或$\frac{11}{12}$.
点评 本题考查正方形的性质、轴对称的性质、全等三角形的判定和性质.勾股定理等知识,解题的关键是学会添加辅助线构造全等三角形解决问题,属于中考常考题型.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△AOB与△COD是位似图形,它们的对应线段之比是1:3.
如图,△AOB与△COD是位似图形,它们的对应线段之比是1:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com