
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½³µ·Ö±š“ÓA”¢BĮ½µŲĶ¬Ź±³ö·¢£¬¼×³µŌČĖŁĒ°ĶłBµŲ£¬µ½“ļBµŲĮ¢¼“ŅŌĮķŅ»ĖŁ¶Č°“ŌĀ·ŌČĖŁ·µ»Ųµ½AµŲ£»ŅŅ³µŌČĖŁĒ°ĶłAµŲ£¬Éč¼×”¢ŅŅĮ½³µ¾ąAµŲµÄĀ·³ĢĪŖy£ØĒ§Ć×£©£¬¼×³µŠŠŹ»µÄŹ±¼äĪŖx£ØŹ±£©£¬yÓėxÖ®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾
£Ø1£©Ēó¼×³µ“ÓAµŲµ½“ļBµŲµÄŠŠŹ»Ź±¼ä£»
£Ø2£©Ēó¼×³µ·µ»ŲŹ±yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³ö×Ō±äĮæxµÄȔֵ·¶Ī§£»
£Ø3£©ĒóŅŅ³µµ½“ļAµŲŹ±¼×³µ¾ąAµŲµÄĀ·³Ģ£®

”¾“š°ø”æ£Ø1£©2.5Š”Ź±£»£Ø2£©y=©100x+550£»£Ø3£©175Ē§Ć×£®
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾ŻĢāŅāĮŠĖćŹ½¼“æɵƵ½½įĀŪ£»
£Ø2£©øł¾ŻĢāŅāĮŠ·½³Ģ×鼓æɵƵ½½įĀŪ£»
£Ø3£©øł¾ŻĢāŅāĮŠĖćŹ½¼“æɵƵ½½įĀŪ£®
ŹŌĢā½āĪö£ŗ£Ø1£©300”Ā£Ø180”Ā1.5£©=2.5£ØŠ”Ź±£©£®
“š£ŗ¼×³µ“ÓAµŲµ½“ļBµŲµÄŠŠŹ»Ź±¼äŹĒ2.5Š”Ź±£»
£Ø2£©Éč¼×³µ·µ»ŲŹ±yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖy=kx+b£¬”ą![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ ![]() £¬”ą¼×³µ·µ»ŲŹ±yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ŹĒy=©100x+550£Ø2.5”Üx”Ü5.5£©£»
£¬”ą¼×³µ·µ»ŲŹ±yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ŹĒy=©100x+550£Ø2.5”Üx”Ü5.5£©£»
£Ø3£©300”Ā[£Ø300©180£©”Ā1.5]=3.75Š”Ź±£¬µ±x=3.75Ź±£¬y=175Ē§Ć×£®
“š£ŗŅŅ³µµ½“ļAµŲŹ±¼×³µ¾ąAµŲµÄĀ·³ĢŹĒ175Ē§Ć×£®


 ÓÅ°Ł·ÖæĪŹ±»„¶ÆĻµĮŠ“š°ø
ÓÅ°Ł·ÖæĪŹ±»„¶ÆĻµĮŠ“š°ø æŖŠÄĶÜדŌŖ×÷ŅµĻµĮŠ“š°ø
æŖŠÄĶÜדŌŖ×÷ŅµĻµĮŠ“š°ø æĪŹ±ÕĘæŲĖęĢĆĮ·Ļ°ĻµĮŠ“š°ø
æĪŹ±ÕĘæŲĖęĢĆĮ·Ļ°ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
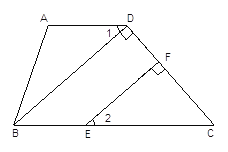
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖıߊĪABCDÖŠ£¬”ĻA=104”ć£”Ļ2£¬”ĻABC=76”ć£«”Ļ2£¬BD”ĶCDÓŚD£¬EF”ĶCDÓŚF£®
ĒóÖ¤£ŗ”Ļ1=”Ļ2£®ĒėÄćĶź³ÉĻĀĆęÖ¤Ć÷¹ż³Ģ£®
Ö¤Ć÷£ŗŅņĪŖ”ĻA£½104”ć£”Ļ2£¬”ĻABC£½76”ć£«”Ļ2£¬£Ø £©
ĖłŅŌ ”ĻA£«”ĻABC£½104”ć£”Ļ2£«76”ć£«”Ļ2£¬ £Ø µČŹ½ŠŌÖŹ £©
¼“ ”ĻA£«”ĻABC£½180”ć
ĖłŅŌ AD”ĪBC£¬£Ø £©
ĖłŅŌ ”Ļ1£½”ĻDBC£¬£Ø £©
ŅņĪŖ BD”ĶDC£¬EF”ĶDC£¬£Ø £©
ĖłŅŌ ”ĻBDC=90”ć,”ĻEFC=90”ć,( )
ĖłŅŌ ”ĻBDC=”ĻEFC,
ĖłŅŌ BD”Ī £¬£Ø £©
ĖłŅŌ ”Ļ2£½”ĻDBC£¬£Ø £©
ĖłŅŌ ”Ļ1£½”Ļ2 £Ø £©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĄķ½ā
”ß![]() £¼
£¼![]() £¼
£¼![]() £¬¼“2£¼
£¬¼“2£¼![]() £¼3£®
£¼3£®
”ą![]() µÄÕūŹż²æ·ÖĪŖ2£¬Š”Źż²æ·ÖĪŖ
µÄÕūŹż²æ·ÖĪŖ2£¬Š”Źż²æ·ÖĪŖ![]() ©2£¬
©2£¬
”ą1£¼![]() ©1£¼2
©1£¼2
”ą![]() ©1µÄÕūŹż²æ·ÖĪŖ1£®
©1µÄÕūŹż²æ·ÖĪŖ1£®
”ą![]() ©1µÄŠ”Źż²æ·ÖĪŖ
©1µÄŠ”Źż²æ·ÖĪŖ![]() ©2
©2
½ā¾öĪŹĢā£ŗŅŃÖŖ£ŗaŹĒ![]() ©3µÄÕūŹż²æ·Ö£¬bŹĒ
©3µÄÕūŹż²æ·Ö£¬bŹĒ![]() ©3µÄŠ”Źż²æ·Ö£¬
©3µÄŠ”Źż²æ·Ö£¬
Ēó£ŗ£Ø1£©a£¬bµÄÖµ£»
£Ø2£©£Ø©a£©3+£Øb+4£©2µÄĘ½·½øł£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ(2016”¤Ģģ½ņ)¹«Ė¾ÓŠ330ĢØ»śĘ÷ŠčŅŖŅ»“ĪŠŌŌĖĖĶµ½Ä³µŲ£¬¼Ę»®×āÓĆ¼×”¢ŅŅĮ½ÖÖ»õ³µ¹²8Į¾£¬ŅŃÖŖĆæĮ¾¼×ÖÖ»õ³µŅ»“Ī×ī¶ąŌĖĖĶ»śĘ÷45ĢØ£¬×ā³µ·ŃÓĆĪŖ400ŌŖ£¬ĆæĮ¾ŅŅÖÖ»õ³µŅ»“Ī×ī¶ąŌĖĖĶ»śĘ÷30ĢØ£¬×ā³µ·ŃÓĆĪŖ280ŌŖ£®
(1)Éč×āÓĆ¼×ÖÖ»õ³µxĮ¾(xĪŖ·ĒøŗÕūŹż)£¬ŹŌĢīŠ“±ķøń£ŗ
±ķŅ»£ŗ
×āÓĆ¼×ÖÖ»õ³µµÄŹżĮæ / Į¾ | 3 | 7 | x |
×āÓĆµÄ¼×ÖÖ»õ³µ×ī¶ąŌĖĖĶ»śĘ÷µÄŹżĮæ / ĢØ | 135 | ||
×āÓƵÄŅŅÖÖ»õ³µ×ī¶ąŌĖĖĶ»śĘ÷µÄŹżĮæ / ĢØ | 150 |
±ķ¶ž£ŗ
×āÓĆ¼×ÖÖ»õ³µµÄŹżĮæ / Į¾ | 3 | 7 | x |
×āÓĆ¼×ÖÖ»õ³µµÄ·ŃÓĆ/ ŌŖ | 2800 | ||
×āÓĆŅŅÖÖ»õ³µµÄ·ŃÓĆ / ŌŖ | 280 |
(2)Čō×āÓĆ¼×ÖÖ»õ³µxĮ¾Ź±£¬ÉčĮ½ÖÖ»õ³µµÄ×Ü·ŃÓĆĪŖyŌŖ£¬ŹŌČ·¶ØÄÜĶź³É“ĖĻīŌĖĖĶČĪĪńµÄ×ī½ŚŹ”·ŃÓƵÄ×ā³µ·½°ø£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĄŗĒņŌĖ¶ÆŌ±Č„Äź¹²²Ī¼Ó40³”±ČČü£¬ĘäÖŠ3·ÖĒņµÄĆüÖŠĀŹĪŖ0.25£¬Ę½¾łĆæ³”ÓŠ12“Ī3·ÖĒņĪ“Ķ¶ÖŠ£®
(1)øĆŌĖ¶ÆŌ±Č„ÄźµÄ±ČČüÖŠ¹²Ķ¶³ö¶ąÉŁøö3·ÖĒņ£æ¹²Ķ¶ÖŠ¶ąÉŁøö3·ÖĒņ£æ
(2)ŌŚĘäÖŠµÄŅ»³”±ČČüÖŠ£¬øĆŌĖ¶ÆŌ±3·ÖĒņ¹²³öŹÖ20“Ī£¬Š”ĮĮĖµ£¬øĆŌĖ¶ÆŌ±Õā³”±ČČüÖŠŅ»¶ØĶ¶ÖŠĮĖ5øö3·ÖĒņ£¬ÄćČĻĪŖŠ”ĮĮµÄĖµ·ØÕżČ·Āš£æĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£ŗ
µćA”¢BŌŚŹżÖįÉĻ·Ö±š±ķŹ¾Į½øöŹża”¢b£¬A”¢BĮ½µć¼äµÄ¾ąĄė¼ĒĪŖ|AB|£¬O±ķŹ¾Ōµć£®µ±A”¢BĮ½µćÖŠÓŠŅ»µćŌŚŌµćŹ±£¬²»·ĮÉčµćAĪŖŌµć£¬ČēĶ¼1£¬Ōņ|AB|=|OB|=|b|=|a-b|£»µ±A”¢BĮ½µć¶¼²»ŌŚŌµćŹ±£¬
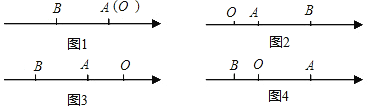
¢ŁČēĶ¼2£¬ČōµćA”¢B¶¼ŌŚŌµćµÄÓŅ±ßŹ±£¬|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|£»
¢ŚČēĶ¼3£¬ČōµćA”¢B¶¼ŌŚŌµćµÄ×ó±ßŹ±£¬|AB|=|OB|-|OA|=|b|-|a|=-b-£Ø-a£©=|a-b|£»
¢ŪČēĶ¼4£¬ČōµćA”¢BŌŚŌµćµÄĮ½±ßŹ±£¬|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|£®
»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©×ŪÉĻĖłŹö£¬ŹżÖįÉĻA”¢BĮ½µć¼äµÄ¾ąĄėĪŖ|AB|=______£®
£Ø2£©ČōŹżÖįÉĻµÄµćA±ķŹ¾µÄŹżĪŖ3£¬µćB±ķŹ¾µÄŹżĪŖ-4£¬ŌņA”¢BĮ½µć¼äµÄ¾ąĄėĪŖ______£»
£Ø3£©ČōŹżÖįÉĻµÄµćA±ķŹ¾µÄŹżĪŖx£¬µćB±ķŹ¾µÄŹżĪŖ-2£¬Ōņ|AB|=______£¬Čō|AB|=3£¬ŌņxµÄÖµĪŖ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠŅ»Ć껿ĪŖ5 ![]() µÄµČŃüČż½ĒŠĪ£¬ĖüµÄŅ»øöÄŚ½ĒŹĒ30”ć£¬ŌņŅŌĖüµÄŃü³¤ĪŖ±ßµÄÕż·½ŠĪµÄĆ껿ĪŖ £®
µÄµČŃüČż½ĒŠĪ£¬ĖüµÄŅ»øöÄŚ½ĒŹĒ30”ć£¬ŌņŅŌĖüµÄŃü³¤ĪŖ±ßµÄÕż·½ŠĪµÄĆ껿ĪŖ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠŅ»æĘ¼¼Š”×é½ųŠŠĮĖ»śĘ÷ČĖŠŠ×ߊŌÄÜŹŌŃ飬ŌŚŹŌŃé³”µŲÓŠA”¢B”¢CČżµćĖ³“ĪŌŚĶ¬Ņ»±ŹÖ±µÄČüµĄÉĻ£¬¼×”¢ŅŅĮ½»śĘ÷ČĖ·Ö±š“ÓA”¢BĮ½µćĶ¬Ź±Ķ¬Ļņ³ö·¢£¬ĄśŹ±7·ÖÖÓĶ¬Ź±µ½“ļCµć£¬ŅŅ»śĘ÷ČĖŹ¼ÖÕŅŌ60Ć×/·ÖµÄĖŁ¶ČŠŠ×ߣ¬ČēĶ¼ŹĒ¼×”¢ŅŅĮ½»śĘ÷ČĖÖ®¼äµÄ¾ąĄėy£ØĆ×£©ÓėĖūĆĒµÄŠŠ×ߏ±¼äx£Ø·ÖÖÓ£©Ö®¼äµÄŗÆŹżĶ¼Ļó£¬Ēė½įŗĻĶ¼Ļ󣬻Ų“šĻĀĮŠĪŹĢā£ŗ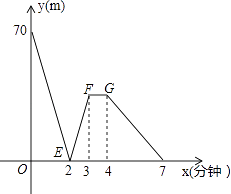
£Ø1£©A”¢BĮ½µćÖ®¼äµÄ¾ąĄėŹĒĆ×£¬¼×»śĘ÷ČĖĒ°2·ÖÖÓµÄĖŁ¶ČĪŖĆ×/·Ö£»
£Ø2£©ČōĒ°3·ÖÖÓ¼×»śĘ÷ČĖµÄĖŁ¶Č²»±ä£¬ĒóĻ߶ĪEFĖłŌŚÖ±ĻßµÄŗÆŹż½āĪöŹ½£»
£Ø3£©ČōĻ߶ĪFG”ĪxÖį£¬Ōņ“Ė¶ĪŹ±¼ä£¬¼×»śĘ÷ČĖµÄĖŁ¶ČĪŖĆ×/·Ö£»
£Ø4£©ĒóA”¢CĮ½µćÖ®¼äµÄ¾ąĄė£»
£Ø5£©Ö±½ÓŠ“³öĮ½»śĘ÷ČĖ³ö·¢¶ą³¤Ź±¼äĻą¾ą28Ć×£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£¾ÅÄź¼¶10øö°ąŹ¦Éś¾ŁŠŠ±ĻŅµĪÄŅÕ»ćŃŻ£¬Ćæ°ą2øö½ŚÄ棬ӊøč³ŖÓėĪčµøĮ½Ąą½ŚÄæ£¬Äź¼¶Ķ³¼Ęŗó·¢ĻÖøč³ŖĄą½ŚÄæŹż±ČĪčµøĄą½ŚÄæŹżµÄ2±¶ÉŁ4øö.
£Ø1£©¾ÅÄź¼¶Ź¦Éś±ķŃŻµÄøč³ŖÓėĪčµøĄą½ŚÄæŹżø÷ÓŠ¶ąÉŁøö£æ
£Ø2£©øĆŠ£Ęß”¢°ĖÄź¼¶Ź¦ÉśÓŠŠ”Ę·½ŚÄæ²ĪÓė£¬ŌŚøč³Ŗ”¢Īčµø”¢Š”Ę·ČżĄą½ŚÄæÖŠ£¬Ćæøö½ŚÄæµÄŃŻ³öĘ½¾łÓĆŹ±·Ö±šŹĒ5·ÖÖÓ”¢6·ÖÖÓ”¢8·ÖÖÓ£¬Ō¤¼ĘĖłÓŠŃŻ³ö½ŚÄæ½»½ÓÓĆŹ±¹²»Ø15·ÖÖÓ.Čō“Ó20£ŗ00æŖŹ¼£¬22£ŗ30Ö®Ē°ŃŻ³ö½įŹų£¬ĪŹ²ĪÓėµÄŠ”Ę·Ąą½ŚÄæ×ī¶ąÄÜÓŠ¶ąÉŁøö£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com