
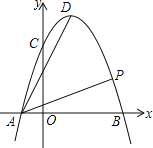
【题目】如图,抛物线y=-x2+2x+3与x轴交于A、B两点,与y轴交于点C,点D为抛物线的顶点,点P为第一象限抛物线上一点,且∠DAP=45°,则点P的坐标为______.
【答案】(![]() ,
,![]() )
)
【解析】
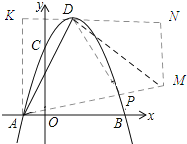
如图所示构造△AKD全等△DNM,先求得点A和点D的坐标,从而可求得点M的坐标,最后求得直线AM的坐标即可.
如图所示:构造△AKD≌△DNM,连接AM.
将y=0代入抛物线的解析式得:-x2+2x+3=0.
解得:x1=3,x2=-1.
∴点A的坐标为(-1,0).
∴点D的横坐标为1.
将x=1代入抛物线的解析式得y=4.
∴AK=4,KD=2,∴DN=4,NM=2.
∴点M的坐标为(5,2).
设直线AM的解析式y=kx+b.将点A、点M的解析式代入得:
![]() ,
,
解得:![]() .
.
∴直线AM的解析式为y=![]() x+
x+![]() .
.
将y=![]() x+
x+![]() 与y=-x2+2x+3联立.
与y=-x2+2x+3联立.
解得:x=![]() ,y=
,y=![]() 或x=-1,y=0(舍去).
或x=-1,y=0(舍去).
∴点P的坐标为(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
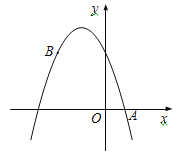
【题目】已知二次函数y1=ax2+bx+c(a≠0)和一次函数y2=kx+n(k≠0)的图象如图所示,下面有四个推断:
①二次函数y1有最大值;
②二次函数y1的图象关于直线x=﹣1对称
③当x=﹣2时,二次函数y1的值大于0
④过动点P(m,0)且垂直于x轴的直线与y1,y2的图象的交点分别为C,D,当点C位于点D上方时,m的取值范围是m<﹣3或m>﹣1.
以上推断正确的是( )
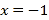
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
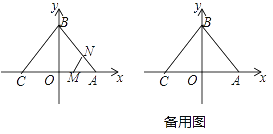
【题目】如图,已知△ABC的顶点坐标分别为A(3,0),B(0,4),C(-3,0).动点M,N同时从A点出发,M沿A→C,N沿折线A→B→C,均以每秒1个单位长度的速度移动,当一个动点到达终点C时,另一个动点也随之停止移动,移动时间记为t秒.连接MN.
(1)求直线BC的解析式;
(2)移动过程中,将△AMN沿直线MN翻折,点A恰好落在BC边上点D处,求此时t值及点D的坐标;
(3)当点M,N移动时,记△ABC在直线MN右侧部分的面积为S,求S关于时间t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
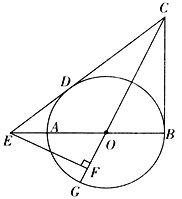
【题目】如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F。
(1)求证:∠FEB=∠ECF
(2)BC= 12, DE=8 求 EA的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
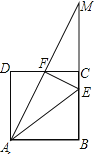
【题目】如图,正方形ABCD中,点E在BC上,且CE=![]() BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=
BC,点F是CD的中点,延长AF与BC的延长线交于点M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF=![]() S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
S四边形ABCF;④∠AFE=90°.其中正确结论的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
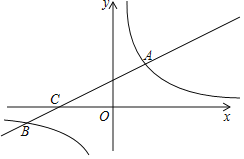
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y=![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
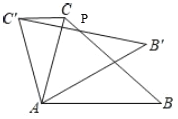
【题目】如图,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,BC与 B′C′交于点P,此时∠BPB′=25°,则∠CAB的大小为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+3的图像经过点A(1,0),B(-2,3).
(1)求该二次函数的表达式;
(2)求该二次函数的最大值;
(3)结合图像,解答问题:当y>3时,x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com