Question

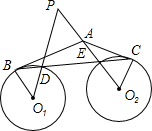
9．如图，AB切⊙O₁于点B，AC切⊙O₂于点C，BC分别交⊙O₁、⊙O₂于点D、E，延长O₁D、O₂E交于点P．若∠BAC=130°，∠ABC=20°，则∠P的度数为（　　）

• A． 30°
• B． 40°
• C． 50
• D． 60°

Answer 1

分析 欲求∠P，只要求出∠PDE以及∠PED，利用切线的性质，圆的半径相等即可解决问题．

解答 解：∵AB、AC是⊙O切线，
∴AB⊥BO₁，AC⊥CO₂，
∴∠ABO₁=90°，∠ACO₂=90°，
∵∠BAC=130°，∠ABC=20°，
∴∠ACB=180°-∠BAC-∠ABC=30°，
∴∠O₁BD=70°，∠O₂CE=60°，
∵O₁B=O₁D，O₂E=O₂C，
∴∠PDE=∠O₁DB=∠O₁BD=70°，∠PED=∠O₂EC=∠O₂CE=60°，
∴∠P=180°-∠PDE-∠PED=50°．
故选C．

点评 本题考查切线的性质、圆、等腰三角形的性质、三角形内角和定理等知识，解题的关键是灵活应用这些知识问题，学会转化的思想，属于中考常考题型．