
【题目】细心观察图形,认真分析各式,然后解答问题:
OA1=1;
OA2=![]() ; S1=
; S1=![]() ×1×1=
×1×1=![]() ;
;
OA3=![]() ; S2=
; S2=![]() ×
×![]() ×1=
×1=![]() ;
;
OA4=![]() ; S3=
; S3=![]() ×
×![]() ×1=
×1=![]() ;
;
(1)推算出OA10= .
(2)若一个三角形的面积是![]() .则它是第 个三角形.
.则它是第 个三角形.
(3)用含n(n是正整数)的等式表示上述面积变化规律;
(4)求出S12+S22+S23+…+S2100的值.

科目:初中数学 来源: 题型:
【题目】如图1,经过原点O的抛物线![]() (a≠0)与x轴交于另一点A(
(a≠0)与x轴交于另一点A(![]() ,0),在第一象限内与直线y=x交于点B(2,t).
,0),在第一象限内与直线y=x交于点B(2,t).
(1)求这条抛物线的表达式;
(2)在第四象限内的抛物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
(3)如图2,若点M在这条抛物线上,且∠MBO=∠ABO,在(2)的条件下,是否存在点P,使得△POC∽△MOB?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)现有5个质地、大小完全相同的小球上分别标有数字﹣1,﹣2,1,2,3.先将标有数字﹣2,1,3的小球放在第一个不透明的盒子里,再将其余小球放在第二个不透明的盒子里.现分别从两个盒子里各随即取出一个小球.
(1)请利用列表或画树状图的方法表示取出的两个小球上数字之和所有可能的结果;
(2)求取出的两个小球上的数字之和等于0的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
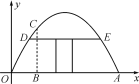
【题目】有一个抛物线型蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示.已知大棚在地面上的宽度OA为8米,距离O点2米处的棚高BC为![]() 米.
米.
(1)求该抛物线的函数关系式;
(2)若借助横梁DE建一个门,要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=∠C,AB=8厘米,BC=6厘米,点D为AB的中点.如果点P在线段BC上以每秒2厘米的速度由B点向C点运动,同时,点Q在线段CA上以每秒a厘米的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3).

(1)用的代数式表示PC的长度;
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(不写作法)已知:如图,在平面直角坐标系中.
(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标;
(2)求△ABC的面积;
(3)在x轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形ABCDE中有一正三角形ACD,若AB=DE,BC=AE,∠E=115°,则∠BAE的度数为何?( )

A. 115 B. 120 C. 125 D. 130
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规画一个角等于已知角,是运用了“全等三角形的对应角相等”这一性质,其全等的依据是( )

A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,已知△ABC中,AC=BC=13,AB=10,△ABC的顶点A、B分别在射线OM、ON上,当点B在ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com