Question

1．如图，在平面直角坐标系中，O是坐标原点，直线AB：y=$\frac{3}{4}x+6$与x，y轴分别相交于点A、B，BC平分∠ABO交x轴于点C．
（1）求点A、B的坐标和线段AB的长；
（2）求线段OC的长；
（3）若过原点的直线l平行于直线AB，动点P在直线l上运动，当∠OBP=$\frac{1}{2}$∠OBA时，求点P的坐标．

Answer 1

分析 （1）对于直线AB解析式，分别令x与y为0求出对应y与x的值，确定出A与B坐标，进而得出OA与OB的长，利用勾股定理求出AB的长即可；
（2）过C作CD⊥AB于点D，如图1所示，利用角平分线定理得到OC=DC，设CO=x，在直角三角形ADC中，利用勾股定理列出关于x的方程，求出方程的解得到x的值，确定出OC的长即可；
（3）记BC与直线l的交点为E，如图2所示，分两种情况考虑：①当点P在OB的左侧时，点P即为BC延长线与直线l的交点，求出直线BC解析式，与直线l解析式联立求出P坐标；②当点P在OB右侧时，∠1=∠2，此时点P为直线BC′与直线l的交点，同理求出P′坐标即可．

解答 解：（1）由直线AB：y=$\frac{3}{4}$x+6，
令y=0得到x=-8，即A（-8，0）；令x=0得到y=6，即B（0，6），
∴OA=8，OB=6，
根据勾股定理得：AB=$\sqrt{{8}^{2}+{6}^{2}}$=10；
（2）过C作CD⊥AB于点D，如图1所示：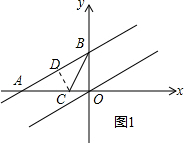

∵BC平分∠ABO，CD⊥AB，CO⊥BO，
∴CD=CO，
设CO=x，在Rt△ADC中，根据勾股定理得：x²+4²=（8-x）²，
解得：x=3，即OC=3；
（3）记BC与直线l的交点为E，

①当点P在OB的左侧时，点P即为BC延长线与直线l的交点，
将B（0，6），C（-3，0）代入y=kx+b得：$\left\{\begin{array}{l}{b=6}\\{-3k+b=0}\end{array}\right.$，
解得：k=2，b=6，即直线BC解析式为y=2x+6，
∵直线l平行于直线AB，
∴直线l为$\frac{3}{4}$x，
联立得：$\left\{\begin{array}{l}{y=2x+6}\\{y=\frac{3}{4}x}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=-\frac{24}{5}}\\{y=-\frac{18}{5}}\end{array}\right.$，即P（-$\frac{24}{5}$，-$\frac{18}{5}$）；
②当点P在OB右侧时，∠1=∠2，此时点P为直线BC′与直线l的交点，
∴直线BC′与直线BC关于y轴对称，
∵C（-3，0），
∴C点关于y轴的对称点C′（3，0），
∴直线BC′解析式为y=-2x+6，
联立得：$\left\{\begin{array}{l}{y=-2x+6}\\{y=\frac{3}{4}x}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=\frac{24}{11}}\\{y=\frac{18}{11}}\end{array}\right.$，即P（$\frac{24}{11}$，$\frac{18}{11}$）．
综上，P的坐标为P（-$\frac{24}{5}$，-$\frac{18}{5}$）或（$\frac{24}{11}$，$\frac{18}{11}$）．

点评 此题属于一次函数综合题，涉及的知识有：待定系数法求一次函数解析式，一次函数与坐标轴的交点，坐标与图形性质，两直线的交点坐标，熟练掌握待定系数法是解本题的关键．