练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】作图题：如图所示是每一个小方格都是边长为1的正方形网格，

    (1)利用网格线作图：

    ①在上找一点P，使点P到和的距离相等；

    ②在射线上找一点Q，使.

    (2)在(1)中连接与，试说明是直角三角形.

    【答案】（1）①详见解析；②详见解析；（2）详见解析．

    【解析】

    （1）根据网格特点作出∠A的角平分线与BC的交点就是点P，作BC的垂直平分线与AP的交点就是点Q．

    （2）首先利用勾股定理计算出CQ2、BQ2、BC2，然后利用勾股定理逆定理可得△CBQ是直角三角形．

    （1）点P就是所要求作的到AB和AC的距离相等的点，点Q就是所要求作的使QB=QC的点．

    （2）连接CQ、BQ．

    ∵CQ2=12+52=26，BQ2=12+52=26，BC2=62+42=36+16=52，∴CQ2+BQ2=BC2，∴∠CQB=90°，∴△CBQ是直角三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线l1∥l2 ， 线段AB在直线l1上，BC垂直于l1交l2于点C，且AB=BC，P是线段BC上异于两端点的一点，过点P的直线分别交l2、l1于点D、E（点A、E位于点B的两侧），满足BP=BE，连接AP、CE．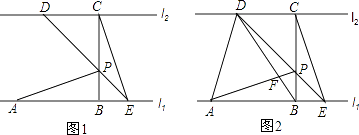

    （1）求证：△ABP≌△CBE；
    （2）连结AD、BD，BD与AP相交于点F．如图2．
    ①当 =2时，求证：AP⊥BD；
    ②当 =n（n＞1）时，设△PAD的面积为S1 ， △PCE的面积为S2 ， 求 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=x2+bx+c的顶点坐标为M（0，﹣1），与x轴交于A、B两点．

    （1）求抛物线的解析式；
    （2）判断△MAB的形状，并说明理由；
    （3）过原点的任意直线（不与y轴重合）交抛物线于C、D两点，连接MC，MD，试判断MC、MD是否垂直，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

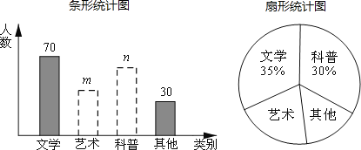
    【题目】在“书香包河”读书活动中，学校准备购买一批课外读物，为使课外读物满足学生们的需求，学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根据调查结果绘制的两幅不完整的统计图．请你根据统计图提供的信息，解答下列问题：

    (1)本次调查中，一共调查了______________名同学；

    (2)条形统计图中，m=_________，n=__________；

    (3)扇形统计图中，艺术类读物所在扇形的圆心角是多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，D为BC边上一点，∠B=30°∠DAB=45°．（1）求∠DAC的度数；（2）请说明：AB=CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在梯形ABCD中，AD∥BC，AB=4，∠C=30°，点E、F分别是边AB、CD的中点，作DP∥AB交EF于点G，∠PDC=90°，求线段GF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上点A表示的数a、点B表示数b，a、b满足|a﹣30|+（b+6）2=0．点O是数轴原点．

    （1）点A表示的数为　 　，点B表示的数为　 　，线段AB的长为　 　．

    （2）若点A与点C之间的距离表示为AC，点B与点C之间的距离表示为BC，请在数轴上找一点C，使AC=2BC，则点C在数轴上表示的数为　 　．

    （3）现有动点P、Q都从B点出发，点P以每秒1个单位长度的速度向终点A移动；当点P移动到O点时，点Q才从B点出发，并以每秒3个单位长度的速度向右移动，且当点P到达A点时，点Q就停止移动，设点P移动的时间为t秒，问：当t为多少时，P、Q两点相距4个单位长度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】移动公司为了方便学生上网查资料，提供了两种上网优惠方法：

    A．计时制：0.08元/分钟；B．包月制：40元/月（只限一台电脑上网）．

    另外，不管哪种收费方式，上网时都得加收通讯费0.03元/分钟．

    （1）设小明某月上网时间为x分钟，请分别用含x的式子表示出两种付费方式下小明应支付的费用；

    （2）一个月上网时间为多少分钟时，两种方式付费一样多？

    （3）如果一个月上网10小时，选择哪种方式更优惠？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察图，下列说法正确的有(　　)

    ①同一平面内，过点A有且只有一条直线AC垂直于直线l；②线段AB，AC，AD中，AC最短，根据是“两点之间的所有连线中，线段最短”；③线段AB，AC，AD中，AC最短，根据是“直线外一点，与直线上各点连接的所有线段中，垂线段最短”；④线段AC的长是点A到直线l的距离．

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    同步练习册答案