
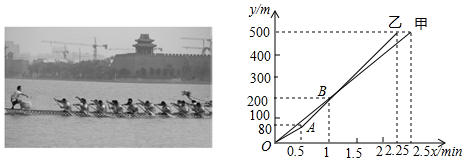
| A. | 乙队比甲队提前0.25min到达终点 | |
| B. | 当乙队划行110m时,此时落后甲队15m | |
| C. | 0.5min后,乙队比甲队每分钟快40m | |
| D. | 自1.5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min |
分析 观察函数图象可知,函数的横坐标表示时间,纵坐标表示路程,根据图象上特殊点的意义即可求出答案.
解答 解:A、由横坐标看出乙队比甲队提前0.25min到达终点,故A不符合题意;
B、乙AB段的解析式为y=240x-40,当y=110时,x=$\frac{5}{8}$;甲的解析式为y=200x,当x=$\frac{5}{8}$时,y=125,当乙队划行110m时,此时落后甲队15m,故B不符合题意;
C、乙AB段的解析式为y=240x-40乙的速度是240m/min;甲的解析式为y=200x,甲的速度是200m/min,0.5min后,乙队比甲队每分钟快40m,故C不符合题意;
D、甲的解析式为y=200x,当x=1.5时,y=300,甲乙同时到达(500-300)÷(2.25-1.5)≈267m/min,故D符合题意;
故选:D.
点评 此题主要考查了函数图象的性质,读函数的图象时首先要理解横纵坐标表示的含义,理解问题叙述的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
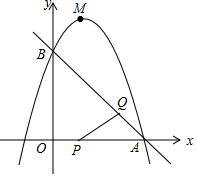 如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线
如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月份n(月) | 1 | 2 |
| 成本y(万元/件) | 11 | 12 |
| 需求量x(件/月) | 120 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
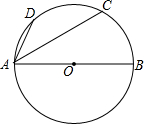 如图,AB为⊙O的直径,C、D为⊙O上的点,$\widehat{AD}$=$\widehat{CD}$.若∠CAB=40°,则∠CAD=25°.
如图,AB为⊙O的直径,C、D为⊙O上的点,$\widehat{AD}$=$\widehat{CD}$.若∠CAB=40°,则∠CAD=25°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com