
分析 (1)根据x2-5x+1=0,通过变形可以得到$x+\frac{1}{x}$的值,从而可以得到x2+$\frac{1}{x^2}$的值;
(2)根据(1)中x2+$\frac{1}{x^2}$的值,可以求得x4+$\frac{1}{x^4}$的值;
(3)根据根据(1)中x2+$\frac{1}{x^2}$的值,可以求得$(x-\frac{1}{x})^{2}$的值,从而可以求得x-$\frac{1}{x}$的值.
解答 解:(1)∵x2-5x+1=0,
∴x2+1=5x,
∴$x+\frac{1}{x}=5$,
∴$(x+\frac{1}{x})^{2}=25$,
∴${x^2}+2+\frac{1}{x^2}=25$,
∴${x^2}+\frac{1}{x^2}=23$;
(2)∵${x^2}+\frac{1}{x^2}=23$,
∴${x}^{4}+2+\frac{1}{{x}^{4}}=529$,
∴${x^4}+\frac{1}{x^4}$=527;
(3)${(x-\frac{1}{x})^2}={(x+\frac{1}{x})^2}-4=21$,
∴$x-\frac{1}{x}=±\sqrt{21}$.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.


 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
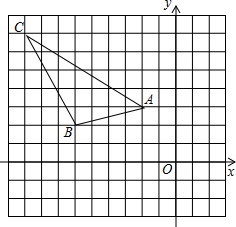 已知,△ABC在平面直角坐标系中的位置如图所示,(正方形网格中每个小正方形的边长为1)
已知,△ABC在平面直角坐标系中的位置如图所示,(正方形网格中每个小正方形的边长为1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小刚学想测量灯杆AB的高度,结果他在D处时用测角仪测灯杆顶端A的仰角
小刚学想测量灯杆AB的高度,结果他在D处时用测角仪测灯杆顶端A的仰角查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC.
如图,AB为半圆O的直径,点C在半圆O上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com