
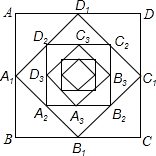
 连结正方形四边中点所构成的正方形,我们称其原正方形的中点正方形,如图,已知正方形ABCD的中点正方形是A1B1C1D1,再作正方形A1B1C1D1的中点正方形A2B2C2D2,…这样不断地作下去,第n次所做的中点正方形 AnBnCnDn,若正方形ABCD的边长为1,则第10次所作的中点正方形边长为$\frac{1}{32}$,若设中点正方形 AnBnCnDn的面积为Sn,则S1+S2+S3+…+S10=$\frac{1023}{1024}$.
连结正方形四边中点所构成的正方形,我们称其原正方形的中点正方形,如图,已知正方形ABCD的中点正方形是A1B1C1D1,再作正方形A1B1C1D1的中点正方形A2B2C2D2,…这样不断地作下去,第n次所做的中点正方形 AnBnCnDn,若正方形ABCD的边长为1,则第10次所作的中点正方形边长为$\frac{1}{32}$,若设中点正方形 AnBnCnDn的面积为Sn,则S1+S2+S3+…+S10=$\frac{1023}{1024}$. 分析 根据勾股定理找出A1B1、A2B2、A3B3的长度,根据数据的变化找出变化规律“AnBn=$(\frac{\sqrt{2}}{2})^{n}$”,依此规律结合正方形的面积公式即可得出结论.
解答 解:观察,发现规律:AB=1,A1B1=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$,A2B2=$\frac{\sqrt{2}}{2}$A1B1=$\frac{1}{2}$,A3B3=$\frac{\sqrt{2}}{2}$A2B2=$\frac{\sqrt{2}}{4}$,…,
∴AnBn=$(\frac{\sqrt{2}}{2})^{n}$.
当n=10时,A10B10=$(\frac{\sqrt{2}}{2})^{10}$=$\frac{1}{32}$.
设S1+S2+S3+…+S10=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{1024}$=S,则$\frac{1}{2}$S=$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{1024}$+$\frac{1}{2048}$,
∴S-$\frac{1}{2}$S=$\frac{1}{2}$-$\frac{1}{2048}$=$\frac{1023}{2048}$,
∴S=$\frac{1023}{1024}$.
故答案为:$\frac{1}{32}$;$\frac{1023}{1024}$.
点评 本题考查了勾股定理、正方形的面积公式以及规律型中图形的变化类,解题的关键是找出变化规律“AnBn=$(\frac{\sqrt{2}}{2})^{n}$”.本题属于中档题,难度不大,解决该题型题目时,根据勾股定理找出部分正方形的边长,根据边长的变化找出变化规律是解题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )
如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 12% |
| 5<x≤10 | 12 | 24% |
| 10<x≤15 | 16 | 32% |
| 15<x≤20 | 10 | 20% |
| 20<x≤25 | 4 | 8% |
| 25<x≤30 | 2 | 4% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 用一个平行于底面的平面去截如图放置的一个圆锥,将其分成上下两个几何体,如果设上面的小圆锥体积为x,下面的圆台体积为y,当截面由顶点向下平移时,y与x满足的函数关系的图象是( )
用一个平行于底面的平面去截如图放置的一个圆锥,将其分成上下两个几何体,如果设上面的小圆锥体积为x,下面的圆台体积为y,当截面由顶点向下平移时,y与x满足的函数关系的图象是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com