练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知（-2，4）是反比例函数图象上一点，下列各点也在该图象上的是（　　）
    A、（-1，3）
    B、（2，4）
    C、（2
    		2
    ，4）
    D、（-4，2）
    分析：将（1，-2）代入y=
    k
    x
    即可求出k的值，再根据k=xy解答即可．
    解答：解：所给点的横纵坐标的积为-2×4=-8，
    A、横纵坐标的积为-1×3=-3，不符合题意；
    B、横纵坐标的积为2×4=8，不符合题意；
    C、横纵坐标的积为2
    		2
    ×4=8
    		2
    ，不符合题意；
    D、横纵坐标的积为-4×2=-8，符合题意；
    故选D．
    点评：本题考查了反比例函数图象上点的坐标特征，只要点在函数的图象上，则一定满足函数的解析式．反之，只要满足函数解析式就一定在函数的图象上．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，已知平行四边形ABCD，E是对角线AC延长线上的一点，
    （1）若四边形ABCD是菱形，求证：BE=DE；
    （2）写出（1）的逆命题，并判断其是真命题还是假命题，若是真命题，试给出证明；若是假命题，试举出反例．

    查看答案和解析>>

    科目：初中数学 来源：2012年初中毕业升学考试（福建厦门卷）数学（带解析） 题型：解答题

    已知：如图，⊙O是△ABC的外接圆，AB为⊙O的直径，弦CD交AB于E，
    ∠BCD＝∠BAC .
    （1）求证：AC＝AD；
    （2）过点C作直线CF，交AB的延长线于点F，若∠BCF＝30°,则结论“CF一定是⊙O的切线”是否正确？若正确，请证明；若不正确，请举反例.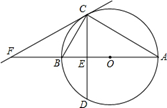

    查看答案和解析>>

    科目：初中数学 来源：2012年初中毕业升学考试（福建厦门卷）数学（解析版） 题型：解答题

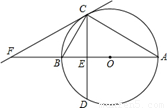
    已知：如图，⊙O是△ABC的外接圆，AB为⊙O的直径，弦CD交AB于E，

    ∠BCD＝∠BAC .

    （1）求证：AC＝AD；

    （2）过点C作直线CF，交AB的延长线于点F，若∠BCF＝30°,则结论“CF一定是⊙O的切线”是否正确？若正确，请证明；若不正确，请举反例.

     

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

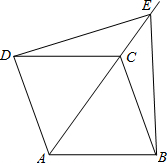    如图，已知平行四边形ABCD，E是对角线AC延长线上的一点，
    （1）若四边形ABCD是菱形，求证：BE=DE；
    （2）写出（1）的逆命题，并判断其是真命题还是假命题，若是真命题，试给出证明；若是假命题，试举出反例．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

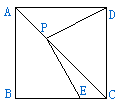
    已知四边形ABCD，点E是BC边上的一个动点（点E不与B、C两点重合），线段BE的垂直平分线交对角线AC于点P，联结DP，PE.

    （1）如图（1），若四边形ABCD是正方形，猜想PD与PE的数量关系，并证明你的结论；

    （2）若四边形ABCD是矩形，（1）中的结论还成立吗？如果成立，证明你的结论；如果不成立，用尺规作图的方法举反例证明（保留作图痕迹，不写作法）；

    （3）若四边形ABCD是矩形，AB＝6，cos∠ACD＝ ，设AP＝x，△PCE的面积为y，求y与x之间的函数关系式.    

     

    查看答案和解析>>

    同步练习册答案