【题目】计算：
①（﹣2x）（4x2﹣2x+1） ②（6a3﹣4a2+2a）÷2a
③a4 +(a2)4 -(a2)2 ④
⑤（2a+b）2 ⑥ (3x+7y)(3x-7y)
【答案】①﹣8x3+4x2﹣2x；②3a2﹣2a+1；③a8；④4；⑤4a2-4ab+b2；⑥9x2-49y2
【解析】试题分析：（1）根据单项式乘以多项式的运算法则直接计算即可；（2）根据多项式乘除以单项式的运算法则直接计算即可；（3）根据幂的乘方和积的乘方运算法计算后合并即可；（4）根据负整数指数幂的性质和0指数幂的性质计算后合并即可；（5）根据完全平方公式直接计算即可；（6）根据平方差公式直接计算即可.
试题解析：
①（﹣2x）（4x2﹣2x+1）
解：（﹣2x）（4x2﹣2x+1）=﹣8x3+4x2﹣2x；
②（6a3﹣4a2+2a）÷2a
解：（6a3﹣4a2+2a）÷2a=3a2﹣2a+1．
③ a4 +(a2)4 -(a2)2
解：原式=a4+a8-a4 =a8
④
解：原式=1+4-1=4
⑤（2a+b）2
解：原式= 4a2-4ab+b2
⑥(3x+7y)(3x-7y)
解：原式=9x2-49y2
手拉手全优练考卷系列答案科目：初中数学 来源： 题型：
【题目】同学们都知道, 
表示
与
之差的绝对值,实际上也可理解为与两数在数轴上所对的两点之间的距离.
试探索：(1)求=______.(2)找出所有符合条件的整数
，使得
这样的整数是_____ ______.(3)由以上探索猜想对于任何有理数，
是否有最小值？如果有，写出最小值；如果没有，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1成中心对称，再作△B2A3B3与△B2A2B1关于点B2成中心对称，如此作下去，则△B2nA2n+1B2n+1（n是正整数）的顶点A2n+1的坐标是 ．
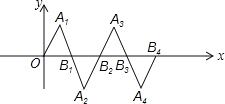
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图1是一个长为2x、宽为2y的长方形，沿图中虚线用剪刀剪成四个完全相同的小长方形，然后按图2所示拼成一个正方形．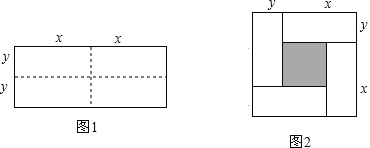
（1）你认为图2中的阴影部分的正方形的边长等于
（2）试用两种不同的方法求图2中阴影部分的面积．
方法1： 方法2：
（3）根据图2你能写出下列三个代数式之间的等量关系吗？
代数式：（x+y）2，（x-y）2，4xy．
（4）根据（3）题中的等量关系，解决如下问题：
若x+y=4，xy=3，则（x-y）2=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图1，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．
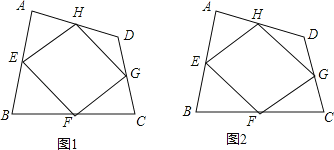
（1）四边形EFGH的形状是 ，证明你的结论．
（2）如图2，请连接四边形ABCD的对角线AC与BD，当AC与BD满足 条件时，四边形EFGH是矩形；证明你的结论．
（3）你学过的哪种特殊四边形的中点四边形是矩形？说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，A、B、C三点的坐标分别为A（﹣6，7）、B（﹣3，0）、C（0，3）．
（1）画出△ABC，
（2）并求△ABC的面积；
（3）在△ABC中，点C经过平移后的对应点为C′（5，4），将△ABC作同样的平移得到△A′B′C′，画出平移后的△A′B′C′；
（4）已知点P（﹣3，m）为△ABC内一点，将点P向右平移4个单位后，再向下平移6个单位得到点Q（n，﹣3），则m=__________n=__________．
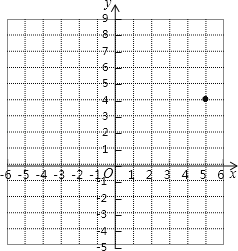
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=x﹣1与反比例函数y=
的图象交于A、B两点，与x轴交于点C，已知点A的坐标为（﹣1，m）．
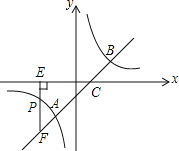
（1）求反比例函数的解析式；
（2）若点P（n，﹣1）是反比例函数图象上一点，过点P作PE⊥x轴于点E，延长EP交直线AB于点F，求△CEF的面积．
（3）在x轴上是否存在点Q，使得△QBC是等腰三角形？若存在，请直接写出Q点坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com