
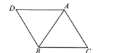
【题目】如图,已知等边![]() ,
,![]() ,将
,将![]() 绕点A顺时针旋转
绕点A顺时针旋转![]() ,得到
,得到![]() ,点E是
,点E是![]() 某边的一点,当
某边的一点,当![]() 为直角三角形时,连接
为直角三角形时,连接![]() ,作
,作![]() 于F,那么
于F,那么![]() 的长度是_________________
的长度是_________________
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,点
运动,点![]() 从点
从点![]() 出发沿
出发沿![]() 向点
向点![]() 运动,点
运动,点![]() 和点
和点![]() 同时出发,速度相同,到达
同时出发,速度相同,到达![]() 点或
点或![]() 点后运动停止.
点后运动停止.
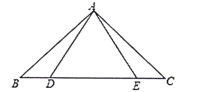
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() 的外心在其内部时,直接写出
的外心在其内部时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
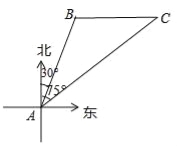
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
![]()
![]() (参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
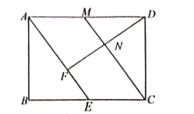
【题目】如图,在矩形![]() 中,点E为
中,点E为![]() 的中点,连接
的中点,连接![]() ,过点D作
,过点D作![]() 于点F,过点C作
于点F,过点C作![]() 于点N,延长
于点N,延长![]() 交
交![]() 于点M.
于点M.
(1)求证:![]()
(2)连接CF,并延长CF交AB于G
①若![]() ,求
,求![]() 的长度;
的长度;
②探究当![]() 为何值时,点G恰好为AB的中点.
为何值时,点G恰好为AB的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的二次函数y=x-bx+![]() b+b-5的图象与x轴有两个公共点.
b+b-5的图象与x轴有两个公共点.
(1)求b的取值范围;
(2)若b取满足条件的最大整数值,当m≤x≤![]() 时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
时,函数y的取值范围是n≤y≤6-2m,求m,n的值;
(3)若在自变量x的值满足b≤x≤b+3的情况下,对应函数y的最小值为![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.
【类比引申】
(1)如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;
【联想拓展】
(2)如图3,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD⊥CD,(点D在⊙O外)AC平分∠BAD.

(1)求证:CD是⊙O的切线;
(2)若DC、AB的延长线相交于点E,且DE=12,AD=9,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com