

分析 (1)先令x=0和y=0分别求A、B两点的坐标,利用勾股定理求AB的长,根据面积法求OF的长;
(2)根据四边形AOBD的面积为38,利用面积和列式可得D的坐标,根据轴对称最短路径:如图2所示:作点A关于y轴的对称点A′(8,0),连接A′D,交y轴于点M,此时△AMD的周长最小,并根据勾股定理求周长的最小值;
(3)分情况讨论:画图根据图形求N、H的坐标.
解答 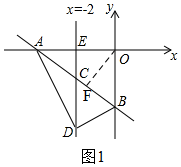 解:(1)如图1,当x=0时,y=-6,
解:(1)如图1,当x=0时,y=-6,
∴B(0,-6),
∴OB=6,
当y=0时,-$\frac{3}{4}$x-6=0,
x=-8,
∴A(-8,0),
∴OA=8,
由勾股定理得:AB=10,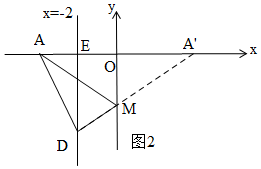
过O作OF⊥AB于F,
S△AOB=$\frac{1}{2}$×6×8=$\frac{1}{2}$×10OF,
∴OF=4.8,
即点O到直线AB的距离是4.8;
(2)如图1,S四边形AOBD=S△ADE+S梯形EDBO=38,
∴$\frac{1}{2}$×(8-2)×(-m)+$\frac{1}{2}$(-m+6)×2=38,
m=-8,
∴D(-2,-8);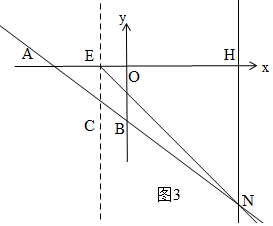
如图2所示:作点A关于y轴的对称点A′(8,0),连接A′D,交y轴于点M,此时△AMD的周长最小,
连接AM,
在Rt△A′ED中,由勾股定理得:A′D=$\sqrt{{8}^{2}+(2+8)^{2}}$=2$\sqrt{41}$,
在Rt△AED中,由勾股定理得:AD=$\sqrt{{6}^{2}+{8}^{2}}$=10,
△AMD的周长=AD+AM+DM=AD+A'M+DM=AD+A'D=10+2$\sqrt{41}$,
即△AMD的周长的最小值是10+2$\sqrt{41}$;
(3)设N(x,-$\frac{3}{4}$x-6),则H(x,0),
①如图3,△EHN为等腰直角三角形,EH=HN,
则x+2=$\frac{3}{4}$x+6,
x=16,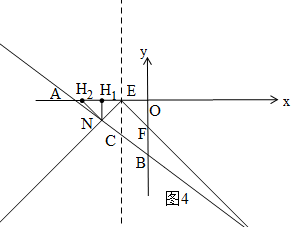
∴H(16,0),N(16,-18);
②如图4,H在E的左侧时,△EHN为等腰直角三角形,EH1=H1N,
则-x-2=$\frac{3}{4}$x+6,
x=-$\frac{32}{7}$,
∴H1(-$\frac{32}{7}$,0),N(-$\frac{32}{7}$,-$\frac{18}{7}$);
同理,H1H2=EH1,
∴△EH2N是等腰直角三角形,
∴N(-$\frac{32}{7}$,-$\frac{18}{7}$),H2(-$\frac{50}{7}$,0);
③如图5,同①得:H(34,0),N(16,-18);
综上所述,H点及对应的N点的坐标有4组:
i)H(16,0),N(16,-18);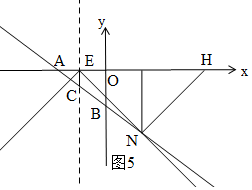
ii)H(-$\frac{32}{7}$,0),N(-$\frac{32}{7}$,-$\frac{18}{7}$);
iii)N(-$\frac{32}{7}$,-$\frac{18}{7}$),H(-$\frac{50}{7}$,0);
iiii)H(34,0),N(16,-18);
点评 本题考查了一次函数的综合应用、三角形的面积、一次函数图象上点的坐标特征、与坐标轴的交点、等腰直角三角形的性质、轴对称的最短路径问题以及勾股定理,解题的关键是:(1)利用面积法求出点O到直线AB的距离;(2)找出△AMD的周长的最小值时,点M的位置;(3)根据等腰直角三角形的性质找出关于x的方程.


科目:初中数学 来源: 题型:解答题
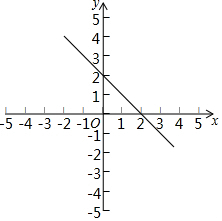 在平面直角坐标系中,直线y=-x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y=-x+2交于点C.
在平面直角坐标系中,直线y=-x+2与y轴交于点A,点A关于x轴的对称点为B,过点B作y轴的垂线l,直线l与直线y=-x+2交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
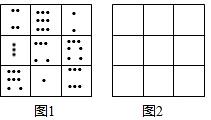 有人建议向火星发射如图1的图案.它叫做幻方,其中9个格中的点数分别是1,2,3,4,5,6,7,8,9.每一横行、每一竖列以及两条斜对角线上的点数的和都是15.如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).
有人建议向火星发射如图1的图案.它叫做幻方,其中9个格中的点数分别是1,2,3,4,5,6,7,8,9.每一横行、每一竖列以及两条斜对角线上的点数的和都是15.如果火星上有智能生物,那么他们可以从这种“数学语言”了解到地球上也有智能生物(人).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com