练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知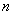是正整数,则奇数可以用代数式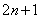来表示.

    (1)分解因式: ;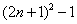

    (2)我们把所有”奇数的平方减去1”所得的数叫”白银数”,则所有”白银数”的最大公约数是多少?请简要说明理由.


    解: (1)

    (2) 所有”白银数”的最大公约数是8

    ∵n正整数,则n与n+1必有一个偶数,∴n(n+1)必是2的倍数,则4n(n+1)必是8的倍数,

    ∴所有”白银数”的最大公约数是8


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知，抛物线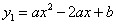经过A(-1，0)，C(2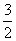，)两点，

    与x轴交于另一点B．

    （1）求此抛物线的解析式；

    （2）若抛物线的顶点为M，点P为线段OB上一动点 （不与点B重合），点Q在线段MB上移动，且∠MPQ=45°，设线段OP=x，MQ=，求y2与x的函数关系式，

    并直接写出自变量x的取值范围．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式x(x+4)+4的结果              ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一次函数，若随的增大而增大，则的值可以是（    ）

    （A）1       （B）2      （C）3      （D）4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     数据1、5、6、5、6、5、6、6的众数是          ，方差是        ． 

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    点A（-1,0）B（4,0）C（0,2）是平面直角坐标系上的三点。

    ① 如图1先过A、B、C作△ABC，然后在在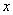轴上方作一个正方形D1E1F1G1,

    使D1E1在AB上， F1、G1分别在BC、AC上

    ② 如图2先过A、B、C作圆⊙M，然后在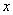轴上方作一个正方形D2E2F2G2,

    使D2E2在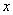轴上 ，F2、G2在圆上

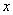    ③ 如图3先过A、B、C作抛物线，然后在轴上方作一个正方形D3E3F3G3,

    使D3E3在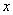轴上， F3、G3在抛物线上

    请比较 正方形D1E1F1G1 , 正方形D2E2F2G2 , 正方形D3E3F3G3 的面积大小

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知两圆的半径长是方程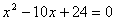的两个解，且两圆的圆心距为d，若两圆相离，则下列结论正确的是(     )

    A．0＜d＜2        B. d＞10         C. 0≤d＜2或d＞10    D.0＜d＜2或d＞10

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在直角坐标系中，O为坐标原点，点A的坐标为（2，2），点C是线段OA上的一个动点（不运动至O，A两点），过点C作CD⊥x轴，垂足为D，以CD为边在右侧作正方形CDEF. 连接AF并延长交x轴的正半轴于点B，连接OF,设OD＝t.

    ⑴tan∠FOB=           ；

    ⑵ 已知二次函数图像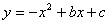 经过O、C、F三点，求二次函数的解析式；

    ⑶ 当t为何值时以B，E，F为顶点的三角形与△OFE相似．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，某超市从底楼到二楼有一自动扶梯，图2是侧面示意图．已知自动扶梯AB的坡度为1：2.4，AB的长度是13米，MN是二楼楼顶，MN∥PQ，C是MN上处在自动扶梯顶端B点正上方的一点，BC⊥MN，在自动扶梯底端A处测得C点的仰角为42°，求二楼的层高BC（精确到0.1米）．（原创）（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）

    查看答案和解析>>

    同步练习册答案