
【题目】如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得到△A′PB.
(1)如图2所示,当PA′⊥BC时,求线段PA的长度.
(2)当∠DPA′=10°时,求∠APB的度数.

【答案】(1)PA=5+5![]() ;(2)85°或95°或5°;
;(2)85°或95°或5°;
【解析】
(1)作BH⊥AD于H.利用特殊直角三角形边角关系 求出AH,BH,即可解决问题.
(2)分情况讨论,求出∠APA′,利用翻折不变性解决问题即可.
解:(1)如图2中,作BH⊥AD于H.
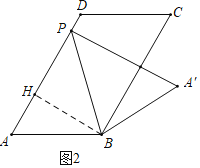
在Rt△ABH中,
∵∠AHB=90°,AB=10,∠A=60°,
∴∠ABH=30°,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵PA′⊥BC,
∴PA′⊥AD,
∴∠APA′=90°,
∴∠HPB=∠BPA′=45°,
∵BH⊥AD,
∴∠HBP=45°,
∴![]() ,
,
∴![]() ;
;
(2)①如图1-1,
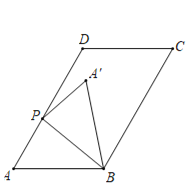
图1-1
当PA′在直线AD的右侧时,
∵∠DPA′=10°,
∴∠APA′=180°﹣∠DPA′=180°﹣10°=170°,
由翻折的性质可知:![]() ;
;
②如图1-2
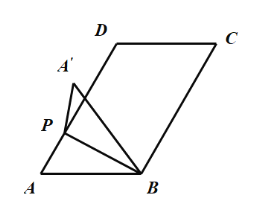
图1-2
当PA′在直线AD的左侧时,由翻折的性质可知:![]() ,
,
③如图1-3
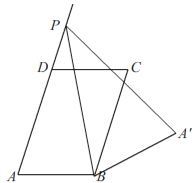
图1-3
当点P在AD的延长线上时,由折叠知,![]() ,
,
故∠APB的度数为85°或95°或5°;


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将放在每个小正方形的边长为1的网格中,点A,B,C均落在格点上.
(1)计算AB边的长等于;
(2)在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使矩形的面积等于△ABC的面积,并简要说明画图的方法(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据我市出租汽车运价与燃料(天然气)价格联动机制,经市政府同意,从2016年11月1日起,市区出租汽车每乘次起步价降低0.5元(不含非用天然气出租车).即排气量1.8L(含1.8L)以下车型由现行起步价3公里9元降低至3公里8.5元;超过3公里每公里运价为2.0元/公里;空驶补贴费为单程载客12公里以上的部分,每公里加收公里运价的50%.
(1)请写出新运价标准下乘车费用y元与乘车距离x公里之间的函数关系式;
(2)小明从家乘车去学校花费了10元,求他家与学校之间的距离是多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
【答案】B
【解析】解析:∵2a4+2b4+c4=2a2c2+2b2c2,∴4a4-4a2c2+c4+4b4-4b2c2+c4=0,
∴(2a2-c2)2+(2b2-c2)2=0,∴2a2-c2=0,2b2-c2=0,
∴c=2a,c=2b,
∴a=b,且a2+b2=c2,
∴△ABC为等腰直角三角形.
故选B.
【题型】单选题
【结束】
11
【题目】将图1中阴影部分的小长方形变换到图2的位置,你能根据两个图形的面积关系得到的数学公式是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
材料1:对于一个关于![]() 的二次三项式
的二次三项式![]() ,除了可以利用配方法求该多项式的取值范围外,爱思考的小川同学还想到了其他的方法;比如先令
,除了可以利用配方法求该多项式的取值范围外,爱思考的小川同学还想到了其他的方法;比如先令![]() ,然后移项可得:
,然后移项可得:![]() ,再利用一元二次方程根的判别式来确定
,再利用一元二次方程根的判别式来确定![]() 的取值范围,请仔细阅读下面的例子:
的取值范围,请仔细阅读下面的例子:
例:求![]() 的取值范围;
的取值范围;
解:令![]()
![]()
![]()
![]()
![]() ;
;
材料2:在学习完一元二次方程的解法后,爱思考的小川同学又想到仿造一元二次方程的解法来解决一元二次不等式的解集问题,他的具体做法如下:
若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 、
、![]() ,则关于
,则关于![]() 的一元二次不等式
的一元二次不等式![]() 的解集为:
的解集为:![]() 或
或![]() ;则关于
;则关于![]() 的一元二次不等式的
的一元二次不等式的![]() 的解集为:
的解集为:![]() .
.
材料3:若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根
有两个不相等的实数根![]() 、
、![]() ;则
;则![]() ;
;![]() ,我们称之为韦达定理;
,我们称之为韦达定理;
请根据上述材料,解答下列问题:
(1)若关于![]() 的二次三项式
的二次三项式![]() (
(![]() 为常数)的最小值为
为常数)的最小值为![]() ,则
,则![]() ________.
________.
(2)求出代数式![]() 的取值范围.
的取值范围.
(3)若关于![]() 的代数式
的代数式![]() (其中
(其中![]() 、
、![]() 为常数,且
为常数,且![]() )的最小值为
)的最小值为![]() ,最大值为4,请求出满足条件的
,最大值为4,请求出满足条件的![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为﹣ ![]()
其中正确的结论个数有( )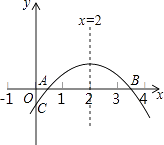
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小楠是一个乐学习,善思考,爱探究的同学,她对函数![]() 的图象和性质进行了探究,请你将下列探究过程补充完整:
的图象和性质进行了探究,请你将下列探究过程补充完整:
(Ⅰ)函数![]() 的自变量x的取值范围是 .
的自变量x的取值范围是 .
(Ⅱ)用描点法画函数图象:
(i)列表:
x | … | ﹣5 | ﹣2 | ﹣1 | 0 | … | 2 | 3 | 4 | 7 | … |
y | … | a | 2 | 3 | b | … | 6 | 3 | 2 | 1 | … |
表中a的值为 ,b的值为 .
(ii)描点连线:请在下图画出该图象的另一部分.

(Ⅲ)观察函数图象,得到函数![]() 的性质:
的性质:
当x 时,函数值y随x的增大而 ;
当x 时,函数值y随x的增大而减少.
(IV)应用:若![]() ≥6,则x的取值范围是 .
≥6,则x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com