
【题目】如图1,在三角形纸板![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的一个点(不与点
上的一个点(不与点![]() 重合),沿
重合),沿![]() 折叠纸板,点
折叠纸板,点![]() 的对应点是点
的对应点是点![]() .
.
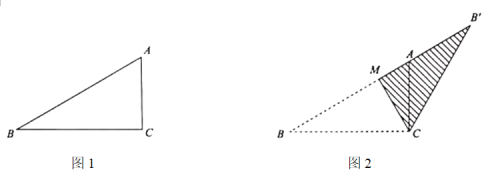
(1)如图2,当点![]() 在射线
在射线![]() 上时,
上时,![]() ________°.
________°.
(2)若![]() ,且点
,且点![]() 不在直线
不在直线![]() 右侧,则点
右侧,则点![]() 到
到![]() 的距离是__________
的距离是__________![]() .
.
【答案】60 ![]()
【解析】
(1)解直角三角形ABC求出∠BAC=60°,得出∠B=30°,由折叠得∠BMC=90°,可得∠BCM;
(2)由折叠得![]() ,∠NCM=∠ACM=45°,根据平角的性质可求得∠BMC=105°,过M作
,∠NCM=∠ACM=45°,根据平角的性质可求得∠BMC=105°,过M作![]() 交BC于点N,得MN=NC,设
交BC于点N,得MN=NC,设![]() ,则
,则![]() ,解Rt△BMN可得BN,根据
,解Rt△BMN可得BN,根据![]() 可得结论
可得结论
(1)如图1,
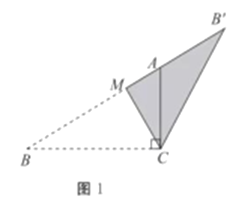
∵在Rt△ABC中,![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∵∠ACB=90°,
∴![]()
当点![]() 在射线
在射线![]() 上时,点
上时,点![]() 是
是![]() 的中点,
的中点,
∴![]() ,即
,即![]()
∴![]() ;
;
故答案为:60;
(2)如图2,
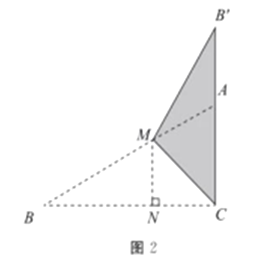
当![]() 时,由折叠得,
时,由折叠得,![]()
设![]() ,
,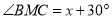
∴![]()
![]() ,
,![]()
∴∠BMC=105°,
过M作![]() 交BC于点N,由折叠得,∠NCM=∠ACM=45°
交BC于点N,由折叠得,∠NCM=∠ACM=45°
∴MN=NC
设![]() cm,则
cm,则![]() cm,
cm,
在Rt△BMN中,∠B=30°,
∴BN=![]()
∴BC=![]() +y=
+y=![]() cm
cm
解得,![]() ,即
,即![]()
∴点M到BC的距离是![]() .
.
故答案为:![]()


科目:初中数学 来源: 题型:
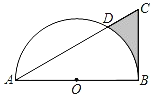
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=4![]() ,∠CAB=30°,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为_____.
,∠CAB=30°,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地为了促进旅游业的发展,要在如图所示的三条公路![]() ,
,![]() ,
,![]() 围成的一块地上修建一个度假村,要使这个度假村到
围成的一块地上修建一个度假村,要使这个度假村到![]() ,
,![]() 两条公路的距离相等,且到
两条公路的距离相等,且到![]() ,
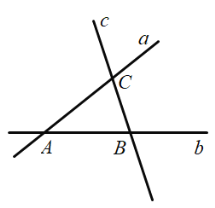
,![]() 两地的距离相等,下列选址方法绘图描述正确的是( )
两地的距离相等,下列选址方法绘图描述正确的是( )
A.画![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,两线的交点符合选址条件
的垂直平分线,两线的交点符合选址条件
B.先画![]() 和
和![]() 的平分线,再画线段
的平分线,再画线段![]() 的垂直平分线,三线的交点符合选址条件
的垂直平分线,三线的交点符合选址条件
C.画三个角![]() ,
,![]() 和
和![]() 三个角的平分线,交点即为所求
三个角的平分线,交点即为所求
D.画![]() ,
,![]() ,
,![]() 三条线段的垂直平分线,交点即为所求
三条线段的垂直平分线,交点即为所求
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上的一点(不与点
上的一点(不与点![]() 重合),边
重合),边![]() 上点
上点![]() 在点
在点![]() 的右边且
的右边且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
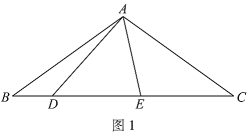
(1)如图1,
①依题意补全图1;
②求证:![]() ;
;
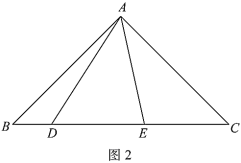
(2)如图2,![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
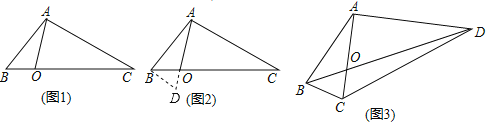
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家经营打印耗材的门店经销各种打印耗材,其中某一品牌硒鼓的进价为![]() 元/个,售价为
元/个,售价为![]() 元/个(
元/个(![]() ).下面是门店在销售一段时间后销售情况的反馈:
).下面是门店在销售一段时间后销售情况的反馈:
①若每个硒鼓按定价30元的8折出售,可获![]() 的利润;
的利润;
②如果硒鼓按30元/个的价格出售,每月可售出500个,在此基础上,售价每增加5元,月销售量就减少50个.
(1)求![]() 的值,并写出该品牌硒鼓每月的销售量
的值,并写出该品牌硒鼓每月的销售量![]() (个)与售价
(个)与售价![]() (元/个)之间的函数关系式,并注明自变量
(元/个)之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(2)求该耗材店销售这种硒鼓每月获得的利润![]() (元)与售价
(元)与售价![]() (元/个)之间的函数关系式,并求每月获得的最大利润;
(元/个)之间的函数关系式,并求每月获得的最大利润;
(3)在新冠肺炎流行期间,这种硒鼓的进价降低为![]() 元/个,售价为
元/个,售价为![]() 元/个(
元/个(![]() ).耗材店在2月份仍然按照销售量与售价关系不变的方式销售,并决定将当月销售这种硒鼓获得的利润全部捐赠给火神山医院,支援武汉抗击新冠肺炎.若要使这个月销售这种硒鼓获得的利润
).耗材店在2月份仍然按照销售量与售价关系不变的方式销售,并决定将当月销售这种硒鼓获得的利润全部捐赠给火神山医院,支援武汉抗击新冠肺炎.若要使这个月销售这种硒鼓获得的利润![]() (元)随售价
(元)随售价![]() (元/个)的增大而增大,请直接写出
(元/个)的增大而增大,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )

A.![]() B.
B.![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
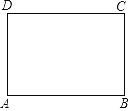
【题目】如图,已知矩形纸片ABCD,怎样折叠,能使边AB被三等分?
以下是小红的研究过程.
思考过程 | 要使边AB被三等分,若从边DC上考虑,就是要折出DM= 也就是要折出DM= 当DB、AM相交于F时,即要折出对角线上的DF= |
折叠方法和示意图 | ①折出DB;对折纸片,使D、B重合,得到的折痕与DB相交于点E;继续折叠纸片,使D、B与E重合,得到的折痕与DB分别相交于点F、G; ②折出AF、CG,分别交边CD、AB于M、Q; ③过M折纸片,使D落在MC上,得到折痕MN,则边AB被N、Q三等分.
|
(1)整理小红的研究过程,说明AN=NQ=QB;
(2)用一种与小红不同的方法折叠,使边AB被三等分.(需简述折叠方法并画出示意图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com