
分析 (1)先把方程化为完全平方的形式,再求出x的值即可;
(2)把A(3,0),B(0,3),对称轴为直线x=1代入二次函数解析式,求出x的值即可.
解答 解:(1)原方程可化为:2(x2-2x+1-1)-1=0,即2(x-1)2=3,
方程两边同时除以2得(x-1)2=$\frac{3}{2}$,
两边开方得x-1=±$\sqrt{\frac{3}{2}}$,
解得x1=1+$\frac{\sqrt{6}}{2}$,x2=1-$\frac{\sqrt{6}}{2}$;
(2)∵抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),对称轴为直线x=1,
∴$\left\{\begin{array}{l}9a+3b+c=0\\ c=3\\-\frac{b}{2a}=1\end{array}\right.$,
解得$\left\{\begin{array}{l}a=-1\\ b=2\\ c=3\end{array}\right.$.
∴二次函数的解析式为:y=-x2+2x+3.
点评 本题考查的是待定系数法求二次函数的解析式,熟知二次函数的对称轴公式是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
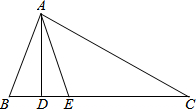 如图,在△ABC中,AD⊥BC,AE平分∠BAC.
如图,在△ABC中,AD⊥BC,AE平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | -2 | D. | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2015=22014.
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2015=22014.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,1) | B. | (-1,1) | C. | (-1,-1) | D. | (1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.
如图,将直线$y=\frac{{\sqrt{3}}}{3}x$向上平移2个单位交坐标轴于点A、D,然后绕AD中点B逆时针旋转60°,三条直线与y轴围成四边形ABCO,若四边形始终覆盖着二次函数y=x2-2mx+m2-1图象的一部分,则满足条件的实数m的取值范围为-$\sqrt{3}$-$\sqrt{2}$≤m≤$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com