
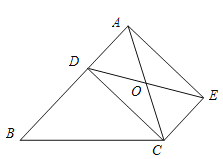
【题目】如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
科目:初中数学 来源: 题型:
【题目】(10分)如图①,在△ABC中,∠ACB=2∠B,AD为∠BAC的角平分线,
求证:AB=AC+CD
小明同学经过思考,得到如下解题思路:
在AB上截取AE=AC,连接DE,得到△ADE≌△ADC,从而易证AB=AC+CD
(1)请你根据以上解思路写出证明过程;
(2)如图②,若AD为△ABC的外角∠CAE平分线,交BC的延长线于点D,
∠D=25°,其他条件不变,求∠B的度数。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a>0)的图象与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C,x1,x2是方程x2+4x﹣5=0的两根.
(1)若抛物线的顶点为D,求S△ABC:S△ACD的值;
(2)若∠ADC=90°,求二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80.
(1)求y关于x的函数解析式;
(2)若该种商品每千克的成本为30元,当每千克的销售价为多少元时,获得的利润为600元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件:
①在足球赛中,弱队战胜强队.
②抛掷1枚硬币,硬币落地时正面朝上.
③任取两个正整数,其和大于1
④长为3cm,5cm,9cm的三条线段能围成一个三角形.
其中确定事件有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DC;③DB=DE;④∠BDE=∠BCA.其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+2S2+2S3+S4=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
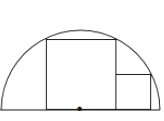
【题目】如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2 , 则该半圆的半径为( )
A. (4+![]() )cm B. 9cm C. 4
)cm B. 9cm C. 4![]() cm D. 6
cm D. 6![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com