
求证:(1)PA=PB+PC;
(2)PA2=BC2+PB·PC;
(3)![]() .
.
| 证明:(1)在PA上截取AE=PB,连结EC.
∵△ABC是等边三角形,∴BC=AC. ∵∠CAE=∠PBC,∴△AEC≌△BPC.∴CE=CP, ∴∠CPA=∠CBA=60°. ∴△PCE是等边三角形. 即PC=PE,∴PA=PB+PC. (2)∵∠BPD=∠APC=60°,∠CAP=∠CBP,∴△PBD∽△PAC. ∴ 又∵∠ABC=∠BPA=60°,∠BAD=∠BAP,∴△PAB∽△BAD. ∴ ①+②,得PA(PD+AD)=AB2+PB·PC 又∵PA=PD+AD,AB=BC,∴PA2=BC2+PB·PC. (3)由(2)中得,PA·PD=PB·PC, ∴ 由PA=PB+PC,代入上式,得 ∴
|
| 证明PA=PB+PC,可在AP上截取AE=BP,然后再证明PE=PC即可.由结论(1)可知,要证明PA2=BC2+PB·PC,只要证明△PBD∽△PAC和△PAB∽
△BAD,得PA·PD=PC·PB,AB2=PA·AD.再结合(1)的结论,即可得证.第(3)问,可先把结论整理变形为
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
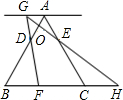 如图,已知:等边三角形ABC的边长为6,点D、E分别在边AB、AC上,且AD=AE=2.点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
如图,已知:等边三角形ABC的边长为6,点D、E分别在边AB、AC上,且AD=AE=2.点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知:等边三角形![]() 的边长为6,点
的边长为6,点 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,且
上,且![]() . 点
. 点 从点
从点![]() 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点![]() 运动的时间为
运动的时间为![]() 秒.当
秒.当![]() 时,直线
时,直线![]() 与过点
与过点![]() 且平行于
且平行于![]() 的直线相交于点
的直线相交于点![]() ,
,![]() 的延长线与
的延长线与![]() 的延长线相交于点
的延长线相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]()
1.用 的代数式表示
的代数式表示![]() ;
;
2.设△ 的面积为
的面积为![]() ,写出
,写出![]() 与
与![]() 的函数关系式;
的函数关系式;
3.当 为何值时,点
为何值时,点![]() 和点
和点![]() 是线段
是线段![]() 的三等分点?
的三等分点?

查看答案和解析>>
科目:初中数学 来源: 题型:
 的边长为6,点
的边长为6,点 、
、 分别在边
分别在边 、
、 上,且
上,且 . 点
. 点 从点
从点 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点 运动的时间为
运动的时间为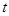 秒. 当
秒. 当 时,直线
时,直线 与过点
与过点 且平行于
且平行于 的直线相交于点
的直线相交于点 ,
, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 ,
, 与
与 相交于点
相交于点
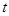 的代数式表示
的代数式表示 ;
; 的面积为
的面积为 ,写出
,写出 与
与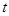 的函数关系式;
的函数关系式;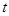 为何值时,点
为何值时,点 和点
和点 是线段
是线段 的三等分点?
的三等分点?
查看答案和解析>>
科目:初中数学 来源:2012届浙江省杭州市余杭瓶窑学区九年级摸底考试数学试卷(带解析) 题型:解答题
如图,已知:等边三角形 的边长为6,点
的边长为6,点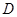 、
、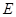 分别在边
分别在边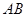 、
、 上,且
上,且 . 点
. 点 从点
从点 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点 运动的时间为
运动的时间为 秒. 当
秒. 当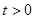 时,直线
时,直线 与过点
与过点 且平行于
且平行于 的直线相交于点
的直线相交于点 ,
, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 ,
,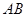 与
与 相交于点
相交于点
【小题1】用 的代数式表示
的代数式表示 ;
;
【小题2】设△ 的面积为
的面积为 ,写出
,写出 与
与 的函数关系式;
的函数关系式;
【小题3】当 为何值时,点
为何值时,点 和点
和点 是线段
是线段 的三等分点?
的三等分点?
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省杭州市余杭瓶窑学区九年级摸底考试数学试卷(解析版) 题型:解答题
如图,已知:等边三角形 的边长为6,点
的边长为6,点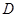 、
、 分别在边
分别在边 、
、 上,且
上,且 . 点
. 点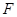 从点
从点 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点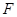 运动的时间为
运动的时间为 秒.
当
秒.
当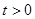 时,直线
时,直线 与过点
与过点 且平行于
且平行于 的直线相交于点
的直线相交于点 ,
, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 ,
, 与
与 相交于点
相交于点
1.用 的代数式表示
的代数式表示 ;
;
2.设△ 的面积为
的面积为 ,写出
,写出 与
与 的函数关系式;
的函数关系式;
3.当 为何值时,点
为何值时,点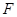 和点
和点 是线段
是线段 的三等分点?
的三等分点?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com